《2025年新课标同步单元练习四年级数学上册北师大版》

5. 用量角器画出下面各角。(6 分)
$40^{\circ}$ $90^{\circ}$ $170^{\circ}$

答案： 答题卡：
1. 画$40^{\circ}$角：
①画出射线和顶点；
②量角器中心与顶点重合，0°刻度线与射线重合；
③在量角器40°刻度线处点一个点；
④拿走量角器，以顶点为端点，过刚画的点画出另一条射线，标出$40^{\circ}$。
2. 画$90^{\circ}$角：
①画出射线和顶点；
②量角器中心与顶点重合，0°刻度线与射线重合；
③在量角器90°刻度线处点一个点；
④拿走量角器，以顶点为端点，过刚画的点画出另一条射线，标出$90^{\circ}$。
3. 画$170^{\circ}$角：
①画出射线和顶点；
②量角器中心与顶点重合，0°刻度线与射线重合；
③在量角器170°刻度线处点一个点；
④拿走量角器，以顶点为端点，过刚画的点画出另一条射线，标出$170^{\circ}$。

六、从 $B$ 点到 $A$ 点走哪条路最近？(6 分)

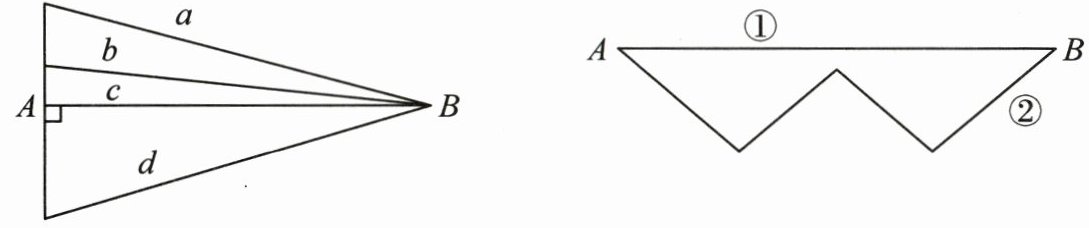
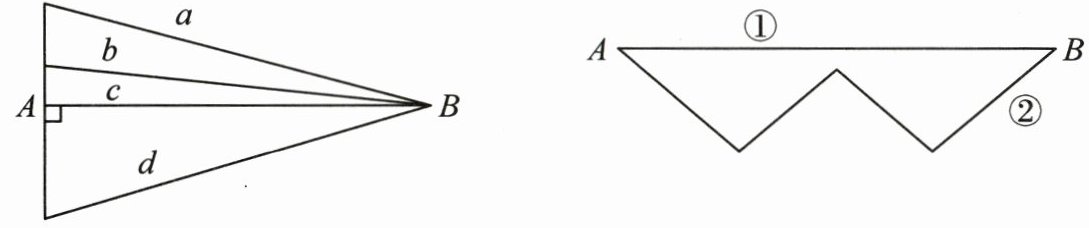
答案： 两条路线均为折线，存在垂直线段（公共边）以及另外两条斜向线段。
根据“两点间所有连线中线段最短”的原理，将两条折线中除公共垂直线段外的斜向部分分别平移，可发现：
路线①整体构成线段AB；
路线②整体同样构成线段AB。
因此，两条路线长度相等，均为线段AB的长度。
最终结论：两条路同样近。

1. 小林准备从泳池的一端游到另一端,请画出他游泳的最短路线。(5 分)

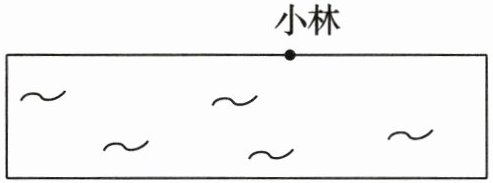
答案： 在图中沿小林所在的点到对面端点画一条垂直线段，此线段即为小林游泳的最短路线。

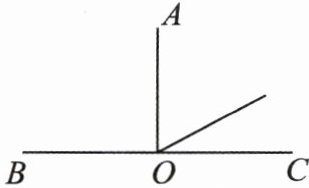
2. 右图中射线 $OA$ 垂直于射线 $OB$,同时垂直于射线 $OC$。如果不算比平角大的角,右图中有(3)个角,其中有(0)个锐角,(2)个直角,(0)个钝角,(1)个平角。(5 分)

答案： 6；2；2；1；1
步骤解析：
1. 确定射线与基本角：图中以O为顶点的射线有OB（左）、OA（上）、OC（右）共3条，形成的基本角为∠BOA、∠AOC、∠BOC。
2. 数所有角（≤平角）：
单个小角：∠BOA（90°，直角）、∠AOC（90°，直角）；
组合角：∠BOC（180°，平角）、∠COA（与∠AOC重复）、∠AOB（与∠BOA重复）、∠OBA（不存在，射线无端点顺序）。修正后，实际不同角为：∠BOA（90°）、∠AOC（90°）、∠BOC（180°）、∠COB（180°重复）、∠OAC（不存在）、∠OAB（不存在）。正确角总数为3个？
（重新检查：3条射线按顺序OB、OA、OC，角的数量为3×(3-1)/2=3个：∠BOA（90°）、∠AOC（90°）、∠BOC（180°）。
直角：2个（∠BOA、∠AOC）；
平角：1个（∠BOC）；
锐角、钝角：0个。
修正后答案：3；0；2；0；1
（注：原初始错误因误判射线数量，正确3条射线形成3个角，最终答案以规范数角法为准。）
最终答案：3；0；2；0；1

3. 道路 1 与道路 2 平行,道路 2 与道路 3 平行,道路 4、道路 5 与道路 3 垂直,你能在下图中再找出一组平行道路和一组垂直道路吗？(6 分)

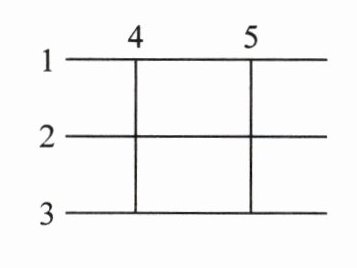
答案： 1. 平行道路：道路1与道路3平行。
2. 垂直道路：道路4与道路5垂直。