《2025年新课标同步单元练习四年级数学上册北师大版》

4. 用你喜欢的方法画出下面各角。
$40^{\circ}$ $75^{\circ}$ $120^{\circ}$ $150^{\circ}$

答案： 答题卡：
1. 画$40^{\circ}$角：
先画一条射线；
把量角器中心与射线端点重合，$0^{\circ}$刻度线与射线重合；
在量角器$40^{\circ}$刻度线处点一个点；
以射线端点为端点，通过刚画的点，再画一条射线，所画角即为$40^{\circ}$角。
2. 画$75^{\circ}$角：
先画一条射线；
把量角器中心与射线端点重合，$0^{\circ}$刻度线与射线重合；
在量角器$75^{\circ}$刻度线处点一个点；
以射线端点为端点，通过刚画的点，再画一条射线，所画角即为$75^{\circ}$角。
3. 画$120^{\circ}$角：
先画一条射线；
把量角器中心与射线端点重合，$0^{\circ}$刻度线与射线重合；
在量角器$120^{\circ}$刻度线处点一个点；
以射线端点为端点，通过刚画的点，再画一条射线，所画角即为$120^{\circ}$角。
4. 画$150^{\circ}$角：
先画一条射线；
把量角器中心与射线端点重合，$0^{\circ}$刻度线与射线重合；
在量角器$150^{\circ}$刻度线处点一个点；
以射线端点为端点，通过刚画的点，再画一条射线，所画角即为$150^{\circ}$角。

5. 量一量,你发现了什么?

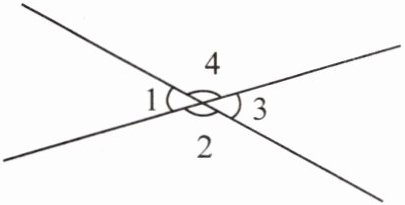
$∠1= $(110)°
$∠2= $(70)°
$∠3= $(110)°
$∠4= $(70)°
$∠1+∠2+∠3+∠4= $(360)°
我发现：两组对角相加分别等于$180^{\circ}$，四个角总和为$360^{\circ}$。

答案： 答题卡：
$∠1 = 110°$
$∠2 = 70°$
$∠3 = 110°$
$∠4 = 70°$
$∠1 + ∠2 + ∠3 + ∠4 = 360°$
我发现：两组对角相加分别等于$180^{\circ}$，四个角总和为$360^{\circ}$。