第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
4. 我国古代数学名著《九章算术》中记载的三角形面积的计算方法是“半广以乘正从”(“广”指三角形的底,“从”指三角形的高)。著名数学家刘徽在注文中还用“以盈补虚”的方法加以说明(如下图)。关于这种推导三角形面积的方法,下列说法错误的是(
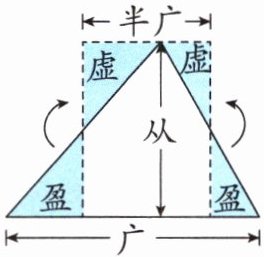
A.三角形的底是长方形宽的2倍
B.长方形的长等于三角形的高
C.长方形的面积是三角形面积的2倍
D.三角形的面积等于三角形底的一半乘三角形的高
C
)。
A.三角形的底是长方形宽的2倍
B.长方形的长等于三角形的高
C.长方形的面积是三角形面积的2倍
D.三角形的面积等于三角形底的一半乘三角形的高
答案:
4. C
5. 下面是3位同学探究梯形的面积计算公式的思路,你能看懂他们的思路吗? 请将他们的思路补充完整。(a表示梯形的上底,b表示梯形的下底,h表示梯形的高,S表示梯形的面积)
(1)

转化为(
(2)

转化为(
(3)
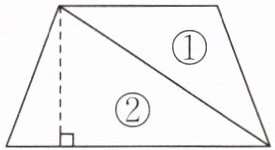
转化为2个(
综上,梯形的面积计算公式用字母表示为(
(1)

转化为(
平行四边
)形,转化后图形的底是(a+b
),高是(h
),面积是((a+b)×h
),所以梯形面积S= ((a+b)×h÷2
)。(2)

转化为(
平行四边
)形,转化后图形的底是(a+b
),高是(h÷2
),面积是((a+b)×h÷2
),所以梯形面积S= ((a+b)×h÷2
)。(3)

转化为2个(
三角
)形,图形①的面积是(a×h÷2
),图形②的面积是(b×h÷2
),所以梯形的面积S= (a×h÷2
)+(b×h÷2
)= ((a+b)×h÷2
)。综上,梯形的面积计算公式用字母表示为(
S=(a+b)×h÷2
)。
答案:
5.
(1)平行四边 $a+b$ h $(a+b)×h$ $(a+b)×h÷2$
(2)平行四边 $a+b$ $h÷2$ $(a+b)×h÷2$ $(a+b)×h÷2$
(3)三角 $a×h÷2$ $b×h÷2$ $a×h÷2$ $b×h÷2$ $(a+b)×h÷2$ $S=(a+b)×h÷2$
(1)平行四边 $a+b$ h $(a+b)×h$ $(a+b)×h÷2$
(2)平行四边 $a+b$ $h÷2$ $(a+b)×h÷2$ $(a+b)×h÷2$
(3)三角 $a×h÷2$ $b×h÷2$ $a×h÷2$ $b×h÷2$ $(a+b)×h÷2$ $S=(a+b)×h÷2$
6. 《九章算术》中用“以盈补虚”的方法计算三角形的面积,请你将下面方格中的梯形也用“以盈补虚”的方法转化成长方形。画一画,并回答下面的问题。
(1)转化后,长方形的士等于梯形的( ),宽等于梯形形的( ),长方形形面积与梯形的面积( )。(最后一空填"相等"或"不相等")
(2)若每个小方格都是边长为1厘米的正方形,则这个梯形形的面积是( )平方厘米。
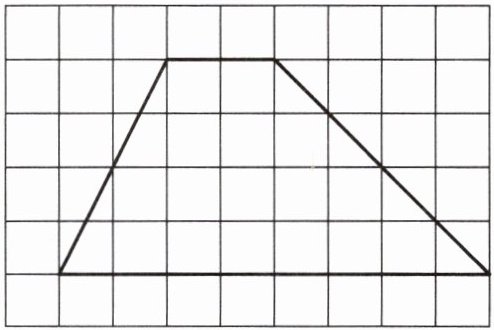
(1)转化后,长方形的士等于梯形的( ),宽等于梯形形的( ),长方形形面积与梯形的面积( )。(最后一空填"相等"或"不相等")
(2)若每个小方格都是边长为1厘米的正方形,则这个梯形形的面积是( )平方厘米。

答案:
6.
(1)上底与下底和的一半 高 相等
(2)20
6.

(1)上底与下底和的一半 高 相等
(2)20
7. 要计算下面虚线左边图形的面积,可以把它割补成已经学过的基本图形。算式“30×12+(9+30)×(20-12)÷2”对应的割补方法是(
B
)。
答案:
7. B
查看更多完整答案,请扫码查看


