9. 某商店销售某种商品,平均每天可售出20件,每件盈利40元。经调查发现,该种商品销售单价每降1元,平均每天可多售出2件。在每件盈利不少于25元的前提下,要获利1200元,每件商品应降价(
A.10元
B.20元
C.10元或20元
D.13元
A
)A.10元
B.20元
C.10元或20元
D.13元
答案:
A
10. 已知关于x的一元二次方程$mx^{2} - (m + 2)x + \frac{m}{4} = 0有两个不相等的实数根x_{1}$,$x_{2}$,若$\frac{1}{x_{1}} + \frac{1}{x_{2}} = 4m$,则m的值是(
A.2
B.-1
C.2或-1
D.不存在
A
)A.2
B.-1
C.2或-1
D.不存在
答案:
A
11.(2024·深圳)已知一元二次方程$x^{2} - 3x + a = 0的一个解为x = 1$,则$a = $
2
。
答案:
2
12.(2024·南通)已知关于x的一元二次方程$x^{2} - 2x + k = 0$有两个不相等的实数根。请写出一个满足题意的k的值:______
0
。
答案:
0(答案不唯一)
13. 有一个人患了禽流感,经过两轮传染后共有169人患了禽流感,每轮传染中平均一个人传染了
12
个人。
答案:
12
14.(2024·东城区模拟)若关于x的一元二次方程$x^{2} - (m + 1)x + m = 0$的两个实数根相差2,则实数m的值是
3或-1
。
答案:
3或-1
15.(2024·南通)如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC = 5$。正方形DEFG的边长为$\sqrt{5}$,它的顶点D,E,G分别在$\triangle ABC$的边上,则BG的长为______
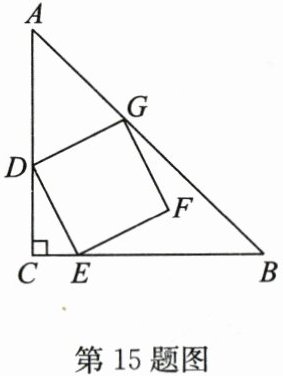
$3\sqrt{2}$
。
答案:
$3\sqrt{2}$
16. 若m,n是一元二次方程$x^{2} + 3x - 1 = 0$的两个实数根,则$\frac{m^{3} + m^{2}n}{3m - 1}$的值为
3
。
答案:
3
17. 已知关于x的方程$x^{2} + \frac{1}{x^{2}} + 2(x + \frac{1}{x}) = 1$,那么$x + \frac{1}{x} + 1$的值为
-2
。
答案:
-2
18.(12分)解下列方程:
(1)$4(1 - x)^{2} = 9$; (2)$2x^{2} - 4x - 3 = 0$(配方法);
(3)$3y^{2} - 2y - 1 = 0$; (4)$x^{2} - 2\sqrt{5}x + 5 = 0$;
(5)$5x(x + 3) = 2(x + 3)$; (6)$(y - 2)(y - 4) = 2$。
(1)$4(1 - x)^{2} = 9$; (2)$2x^{2} - 4x - 3 = 0$(配方法);
(3)$3y^{2} - 2y - 1 = 0$; (4)$x^{2} - 2\sqrt{5}x + 5 = 0$;
(5)$5x(x + 3) = 2(x + 3)$; (6)$(y - 2)(y - 4) = 2$。
答案:
(1)原方程可化为$1-x=\pm \frac{3}{2}$,$\therefore x_{1}=\frac{5}{2}$,$x_{2}=-\frac{1}{2}$.
(2)原方程可化为$x^{2}-2x-1.5=0$,即$(x-1)^{2}=\frac{5}{2}$,则$x-1=\pm \frac{\sqrt{10}}{2}$,$\therefore x_{1}=1+\frac{\sqrt{10}}{2}$,$x_{2}=1-\frac{\sqrt{10}}{2}$.
(3)原方程可化为$(3y+1)(y-1)=0$,$\therefore y_{1}=-\frac{1}{3}$,$y_{2}=1$.
(4)原方程可化为$(x-\sqrt{5})^{2}=0$,$\therefore x_{1}=x_{2}=\sqrt{5}$.
(5)原方程可化为$(x+3)(5x-2)=0$,$\therefore x_{1}=-3$,$x_{2}=\frac{2}{5}$.
(6)原方程可化为$y^{2}-6y+6=0$,即$(y-3)^{2}=3$,则$y-3=\pm \sqrt{3}$,$\therefore y_{1}=3+\sqrt{3}$,$y_{2}=3-\sqrt{3}$.
(1)原方程可化为$1-x=\pm \frac{3}{2}$,$\therefore x_{1}=\frac{5}{2}$,$x_{2}=-\frac{1}{2}$.
(2)原方程可化为$x^{2}-2x-1.5=0$,即$(x-1)^{2}=\frac{5}{2}$,则$x-1=\pm \frac{\sqrt{10}}{2}$,$\therefore x_{1}=1+\frac{\sqrt{10}}{2}$,$x_{2}=1-\frac{\sqrt{10}}{2}$.
(3)原方程可化为$(3y+1)(y-1)=0$,$\therefore y_{1}=-\frac{1}{3}$,$y_{2}=1$.
(4)原方程可化为$(x-\sqrt{5})^{2}=0$,$\therefore x_{1}=x_{2}=\sqrt{5}$.
(5)原方程可化为$(x+3)(5x-2)=0$,$\therefore x_{1}=-3$,$x_{2}=\frac{2}{5}$.
(6)原方程可化为$y^{2}-6y+6=0$,即$(y-3)^{2}=3$,则$y-3=\pm \sqrt{3}$,$\therefore y_{1}=3+\sqrt{3}$,$y_{2}=3-\sqrt{3}$.
查看更多完整答案,请扫码查看


