《2025年练出好成绩四年级数学上册人教版》

1. 在括号里填上适当的面积单位。

答案： 1.平方千米 公顷

(1)9000 公顷 = (90) 平方千米
60 平方千米 = (6000) 公顷
5 平方千米 = (500) 公顷 = (5000000) 平方米
7 平方米 = (700) 平方分米 = (70000) 平方厘米

答案： 2.
(1)90 6000 500 5000000 700 70000

(2)边长是 1000 米的正方形，它的面积是 (1) 平方千米，合 (100) 公顷。

答案： 2.
(2)1 100

(3)“鸟巢”的占地面积约是 20 (公顷)，(5) 个“鸟巢”的占地面积是 1 平方千米。

答案： 2.
(3)公顷 5

3. 在$◯$里填上“＞”“＜”或“=”。
80000 公顷$◯$8 平方千米
2 公顷$◯$200000 平方米
3 平方千米$◯$300 公顷
40000 平方米$◯$40 平方千米

答案： 3.＞ ＜ ＝ ＜

4. 把下面的面积按照从小到大的顺序排列。

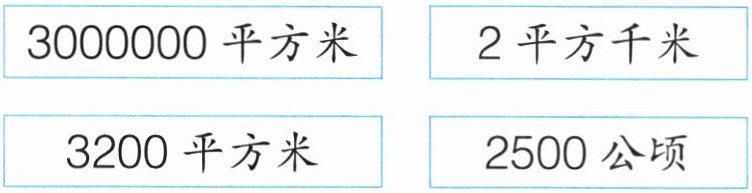
答案： 4.3200平方米＜ 2平方千米＜ 3000000平方米＜ 2500公顷

5. 一个长方形自然保护区，长 9 千米，宽 4 千米，这个保护区的占地面积是多少平方千米？合多少公顷？如果每 20 公顷设立一个保护站，需要几个这样的保护站？

答案： 5.9×4 = 36（平方千米）
36平方千米 = 3600公顷
3600÷20 = 180(个)

6. 一块长方形土地，如果它的长增加 3 千米，宽不变，面积就增加 21 平方千米；如果它的宽增加 5 千米，长不变，面积就增加 40 平方千米。如果这块土地的长和宽同时增加 2 千米，这块土地的面积增加了多少公顷？

答案： 6.21÷3 = 7(千米) 40÷5 = 8(千米)
8×7 = 56(平方千米)
(8 + 2)×(7 + 2) = 90(平方千米)
90 - 56 = 34(平方千米) = 3400(公顷)
解析 由长增加的数及增加的面积可求出原长方形土地的宽，由宽增加的数及增加的面积可求出原长方形土地的长，进而可求解。