《2025年千里马单元测试卷五年级数学下册人教版》

一、看图填一填。（7分）

1. 图①绕点O旋转( )度得到图②。
2. 图③绕点A经过( )时针旋转( )度得到图④。
3. 图⑤经过( )得到图⑥。
4. 图⑦经过( )时针旋转( )度，再平移( )格得到图⑧。

答案： 1.90 2.顺 90 3.平移 4.逆 90 7

1. 电梯的上下运动属于( )现象；电风扇的扇叶转动是( )现象。

答案： 平移 旋转

2.

(1)指针从“12”绕点O顺时针旋转30°到“( )”。
(2)指针从“1”绕点O顺时针旋转______°到“5”。
(3)指针从“6”绕点O逆时针旋转90°到“( )”。
(4)指针从“9”绕点O逆时针旋转______°到“7”。

答案：
(1)1
(2)120
(3)3
(4)60

3.

(1)图形1绕点O顺时针旋转90°到图形( )所在的位置。
(2)图形2绕点O顺时针旋转180°到图形( )所在的位置。
(3)图形3绕点O顺时针旋转( )到图形1所在的位置。
(4)图形1绕点O( )旋转( )到图形4所在的位置。

答案：
(1)2
(2)4
(3)180°
(4)逆时针 90°(答案不唯一)

1. 想一想，下列哪一组都是旋转现象( )。
A. 拉抽屉，电风扇转动
B. 转动转盘，风车转动
C. 时针转动，电梯升降

答案： B

2. 看一看，下面的图②是由图①( )变化得到的图案。

答案： A

3. 下面的图案，( )是由涂有阴影的部分旋转形成的。

答案： B

4. 下面每组中的两个图形，经过平移后，可以完全重合的是( )。

答案： C

5. ，沿顺时针方向旋转90°以后得到的图形是( )。

答案： A

6. 从12时到12时30分，分针绕中心点( )。
A. 逆时针旋转了90°
B. 顺时针旋转了90°
C. 顺时针旋转了180°

答案： C

四、观察下面图形。（12分）

1. 说一说怎样通过平移或旋转让上图变成一个长方形。（6分）
2. 通过平移和旋转上图还能变成什么图形？（6分）

答案： 1. 把②号图绕点O顺时针旋转90°,先向左平移1格,再向上平移2格。(答案不唯一) 2. 平行四边形

1. 先将下图向上平移4格后，再向右平移5格，画出两次平移后的图形。(6分)

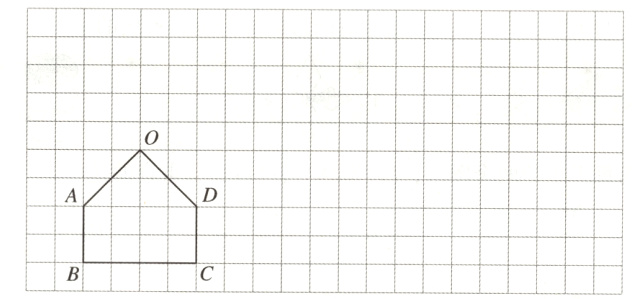
答案： 略

2. 画出三角形绕点O逆时针旋转90°后的图形。(8分)

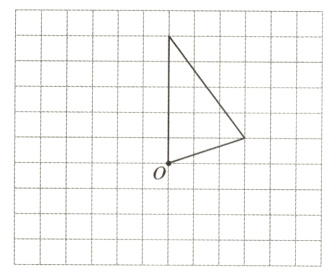
答案： 略

3. 画出下面图形绕点B顺时针旋转90°后的图形。(8分)

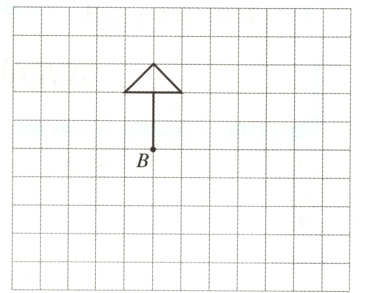
答案： 略

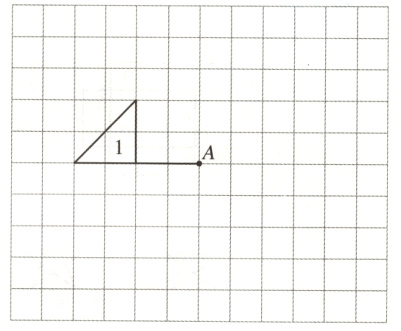
4. 按要求画图。(12分)
(1)把图1绕点A逆时针旋转90°，得到图2。
(2)把图2绕点A逆时针旋转90°，得到图3。
(3)把图1绕点A顺时针旋转90°，得到图4。

答案： 略

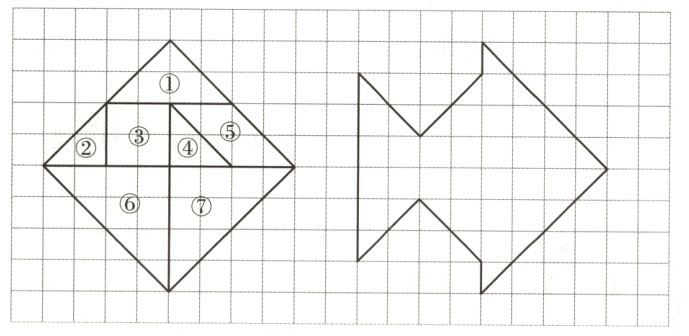
5. 七巧板经过平移或旋转得到了右边的图形。请在右图中画出相应的每块板的轮廓线，并标出序号。(7分)

答案： 略

一、小明折纸飞机用了一张纸的$\frac{1}{2}$，小亮折纸船用了这张纸的$\frac{1}{4}$。（11分）
1. 他们一共用了这张纸的几分之几？
$\frac{1}{2}+\frac{1}{4}=\frac{2}{4}+\frac{1}{4}=\frac{(\ \ \ \ \ )+(\ \ \ \ \ )}{(\ \ \ \ \ )}=\frac{(\ \ \ \ \ )}{(\ \ \ \ \ )}$
2. 小明比小亮多用了这张纸的几分之几？
$\frac{1}{2}-\frac{1}{4}=\frac{(\ \ \ \ \ )}{(\ \ \ \ \ )}-\frac{(\ \ \ \ \ )}{(\ \ \ \ \ )}=\frac{(\ \ \ \ \ )}{(\ \ \ \ \ )}$

答案： 1. $\frac{1}{2}+\frac{1}{4}=\frac{2}{4}+\frac{1}{4}=\frac{(2)+(1)}{(4)}=\frac{(3)}{(4)}$
2. $\frac{1}{2}-\frac{1}{4}=\frac{2}{4}-\frac{1}{4}=\frac{1}{4}$

二、怎样算简便就怎样算。（6分）
根据加法( )律和( )律，先把( )分母分数的两个分数相加比较简便。
$\frac{3}{5}+\frac{7}{10}+\frac{2}{5}=(\underline{\ \ \ \ \ \ }+\underline{\ \ \ \ \ \ })+\frac{7}{10}=(\ \ \ \ \ \ )$

答案： 交换 结合 同
$\frac{3}{5}+\frac{7}{10}+\frac{2}{5}=(\frac{3}{5}+\frac{2}{5})+\frac{7}{10}=1\frac{7}{10}$

三、一杯果汁，明明喝了$\frac{1}{2}$杯，加满水后，又喝了半杯果汁。明明一共喝了多少杯果汁？多少杯水？（8分）
第一次喝了$\frac{1}{2}$杯，还剩$\frac{1}{2}$杯果汁，再加满水后，杯子里有半杯果汁半杯水，又喝了半杯果汁，这次的果汁里既有水，又有果汁。就相当于喝了$\frac{1}{4}$杯果汁。一共喝的果汁是( + )杯。
果汁：
水：

答案： $\frac{1}{2}+\frac{1}{4}$ 果汁：$\frac{1}{2}+\frac{1}{4}=\frac{3}{4}$(杯)
水：$\frac{1}{4}$杯