【题目】如图,平面直角坐标系中A(0,a),B(b,0),且a、b满足![]() 作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.
作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.

(1)求点A、B的坐标;
(2)设△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)点M为线段OP的中点,连接AM,当点P在线段BA上时,△AOM的面积为△AOB面积的![]() 时,求出t值,并求出点M到x轴距离.
时,求出t值,并求出点M到x轴距离.
参考答案:
【答案】(1)A(0,6),B(﹣8,0);(2)S=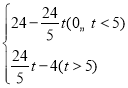 ;(3)t=
;(3)t=![]() ,点M到x轴距离为1.
,点M到x轴距离为1.
【解析】
(1)解二元一次方程组,即可得到A,B坐标;
(2)根据点P的位置,分点P在线段AB上和点P在线段BA延长线上进行讨论,作![]() ,使用
,使用![]() 的面积,进行等面积转化,求出
的面积,进行等面积转化,求出![]() 长度,表示出
长度,表示出![]() 长度,则
长度,则![]() ;
;
(3)由M为OP中点可知,![]() ,结合
,结合![]() ,推出
,推出![]() ,得到
,得到![]() ,求出运动时间t;由M为OP中点,得
,求出运动时间t;由M为OP中点,得![]() ,从而得到点M到
,从而得到点M到![]() 轴的距离.
轴的距离.
(1)由![]() ,解得
,解得![]() ,
,
∴A(0,6),B(﹣8,0).
(2)∵AB=10,
∴点P从B运动到A的时间为5秒,
当0≤t<5时,如图1中,作OH⊥AB于H.
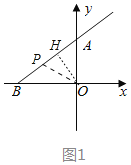
∵S△AOB=![]() OAOB=
OAOB=![]() ABOH,
ABOH,
∴OH=![]() =
=![]()
S=![]() PAOH=
PAOH=![]() (10﹣2t)×
(10﹣2t)×![]() =24﹣
=24﹣![]() t.
t.
当t>5时,S=![]() PAOH=
PAOH=![]() (2t﹣10)×
(2t﹣10)×![]() =
=![]() t﹣24.
t﹣24.
综上所述,S=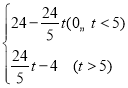 .
.
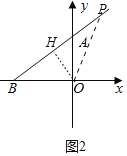
(3)如图3中,连接BM.
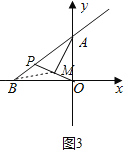
∵OM=PM,
∴S△AOM=S△APM,
∵S△AOM=![]() S△AOB,
S△AOB,
∴S△OPB=![]() S△AOB,
S△AOB,
∴BP=![]() AB,
AB,
∴2t=![]() ,
,
∴t=![]() ,
,
设点M到x轴的距离为h.
∵OM=PM,
∴S△OBM=![]() S△OPB=
S△OPB=![]() S△AOB,
S△AOB,
∴![]() ×8×h=
×8×h=![]() ×
×![]() ×6×8,
×6×8,
解得h=1,
∴点M到x轴距离为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F,连接OC、FC.

(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形AOCF是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.

(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD , 请求出P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.

(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+6分别交x轴、y轴于A、B两点,抛物线y=﹣
x+6分别交x轴、y轴于A、B两点,抛物线y=﹣  x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.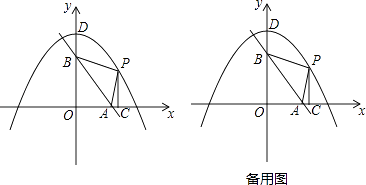
(1)点A的坐标为 , 点D的坐标为;
(2)探究发现:
①假设P与点D重合,则PB+PC=;(直接填写答案)
②试判断:对于任意一点P,PB+PC的值是否为定值?并说明理由;
(3)试判断△PAB的面积是否存在最大值?若存在,求出最大值,并求出此时点P的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为
 ,
,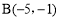 ,
, ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形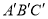 .
. (1)画出三角形ABC和平移后
 的图形;
的图形;(2)写出三个顶点
 ,
, ,
, 的坐标;
的坐标;(3)求三角形ABC的面积.

相关试题

