【题目】如图,直线y=﹣ ![]() x+6分别交x轴、y轴于A、B两点,抛物线y=﹣
x+6分别交x轴、y轴于A、B两点,抛物线y=﹣ ![]() x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.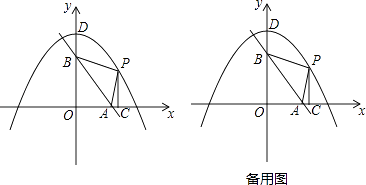
(1)点A的坐标为 , 点D的坐标为;
(2)探究发现:
①假设P与点D重合,则PB+PC=;(直接填写答案)
②试判断:对于任意一点P,PB+PC的值是否为定值?并说明理由;
(3)试判断△PAB的面积是否存在最大值?若存在,求出最大值,并求出此时点P的坐标;若不存在,说明理由.
参考答案:
【答案】
(1)(4,0),(0,8)
(2)PB+PC=10,是,理由如下:过点P作PQ⊥y轴于点Q,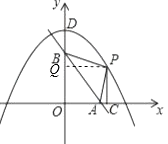 ∵P在抛物线上,且在第一象限,∴设P点坐标为(x,﹣
∵P在抛物线上,且在第一象限,∴设P点坐标为(x,﹣ ![]() x2+8).则PQ=x,PC=﹣
x2+8).则PQ=x,PC=﹣ ![]() x2+8.当4≤x<8时,PB=
x2+8.当4≤x<8时,PB= ![]() =
= ![]() x2+2,∴PB+PC=
x2+2,∴PB+PC= ![]() x2+2+(﹣
x2+2+(﹣ ![]() x2)+8=10,当0<x<4时,同理可得;
x2)+8=10,当0<x<4时,同理可得;
(3)△PAB的面积存在最大值,且最大值为13,此时点P的坐标为(6, ![]() )
)
解:存在.
设△PAB的面积为S.
由(2)假设.
当4≤x<8时,有S= ![]()
=﹣ ![]() x2+3x+4=﹣
x2+3x+4=﹣ ![]() (x﹣6)2+13.
(x﹣6)2+13.
当0<x<4时,s=﹣ ![]() (x﹣6)2+13.
(x﹣6)2+13.
当x=6时,S最大=13,y=﹣ ![]() ×36+8=
×36+8= ![]() ,
,
∴△PAB的面积存在最大值,且最大值为13,此时点P的坐标为(6, ![]() )
)
【解析】
解:(1)y=﹣ ![]() x+6当y=0时,x=4,即A(4,0),
x+6当y=0时,x=4,即A(4,0),
y=﹣ ![]() x2+8当x=0时,y=8,即D点坐标(0,8),
x2+8当x=0时,y=8,即D点坐标(0,8),
所以答案是:(4,0),(0,8);(2)①PB=PO﹣OB=8﹣6=2,PB+PC=8+2=10;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.

(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD , 请求出P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中A(0,a),B(b,0),且a、b满足
 作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.
作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.
(1)求点A、B的坐标;
(2)设△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)点M为线段OP的中点,连接AM,当点P在线段BA上时,△AOM的面积为△AOB面积的
 时,求出t值,并求出点M到x轴距离.
时,求出t值,并求出点M到x轴距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.

(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为
 ,
,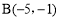 ,
, ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形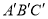 .
. (1)画出三角形ABC和平移后
 的图形;
的图形;(2)写出三个顶点
 ,
, ,
, 的坐标;
的坐标;(3)求三角形ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )
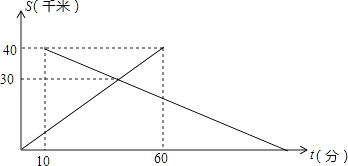
A.14:00
B.14:20
C.14:30
D.14:40 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 的边
的边 、
、 为边的等边三角
为边的等边三角 和等边三角形
和等边三角形 ,四边形
,四边形 是平行四边形.
是平行四边形.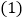 当
当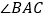 满足什么条件时,四边形
满足什么条件时,四边形 是矩形;
是矩形; 当
当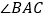 满足什么条件时,平行四边形
满足什么条件时,平行四边形 不存在;
不存在; 当
当 分别满足什么条件时,平行四边形
分别满足什么条件时,平行四边形 是菱形,正方形?
是菱形,正方形?
相关试题

