【题目】解不等式组: ![]() ,并求出它的所有整数解的和.
,并求出它的所有整数解的和.
参考答案:
【答案】解: ![]() ,
,
解不等式①得x>2,
解不等式②得x≤5,
∴原不等式组的解集是2<x≤5,
∴原不等式组的整数解是3,4,5,
∴所有整数解的和3+4+5=12
【解析】解不等式①得x>2,解不等式②得x≤5,所以原不等式组的解集是2<x≤5,即原不等式组的整数解是3,4,5,所有整数解的和3+4+5=12.
【考点精析】解答此题的关键在于理解一元一次不等式组的解法的相关知识,掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ),以及对一元一次不等式组的整数解的理解,了解使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD的对角线相交于点O,AC=
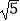 ,CD=1,
,CD=1,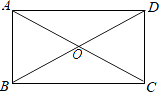
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,∠1 =∠2,∠BAC = 75°将求∠AGD的过程填写完整
解:∵EF∥AD
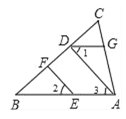
∴ ∠2 = ( )
又∵ ∠1 = ∠2
∴ ∠1 = ∠3。( )
∴AB∥ 。( )
∴∠BAC + = 180°。( )
∵∠BAC=75°∴∠AGD = 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠3=B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
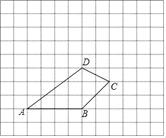
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A′B′C′D′.
(2)求线段AB扫过的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
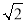 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此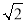 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用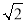 ﹣1来表示
﹣1来表示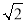 的小数部分,因为
的小数部分,因为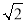 的整数部分是1,将这个数减去其整数部分,差就是小数部分又例如:因为
的整数部分是1,将这个数减去其整数部分,差就是小数部分又例如:因为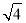 <
<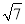 <
<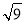 ,即2<
,即2<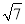 <3,所以
<3,所以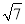 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(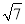 ﹣2)
﹣2)请解答:
(1)
 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;(2)如果
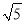 的小数部分为a,
的小数部分为a,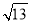 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣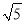 的值.
的值.
相关试题

