【题目】如图,EF∥AD,∠1 =∠2,∠BAC = 75°将求∠AGD的过程填写完整
解:∵EF∥AD
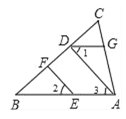
∴ ∠2 = ( )
又∵ ∠1 = ∠2
∴ ∠1 = ∠3。( )
∴AB∥ 。( )
∴∠BAC + = 180°。( )
∵∠BAC=75°∴∠AGD = 。
参考答案:
【答案】详见解析.
【解析】
先根据两直线平行同位角相等可得∠2=∠3,然后根据等量代换可得∠1=∠3,然后根据内错角相等两直线平行可得AB∥DG,然后根据两直线平行同旁内角互补可得∠BAC+∠AGD=180°,进而可求∠AGD的度数.
解:∵EF∥AD
∴∠2=∠3(两直线平行同位角相等)
又∵∠1=∠2
∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等两直线平行)
∴∠BAC+∠AGD=180°(两直线平行同旁内角互补)
∵∠BAC=75°
∴∠AGD=105°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
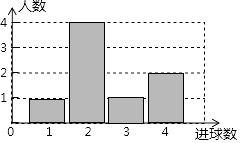
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的概率? -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD的对角线相交于点O,AC=
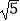 ,CD=1,
,CD=1,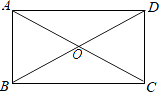
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
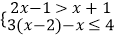 ,并求出它的所有整数解的和.
,并求出它的所有整数解的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠3=B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
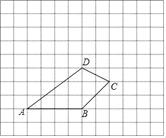
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A′B′C′D′.
(2)求线段AB扫过的面积。
相关试题

