【题目】已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△AˊBD.
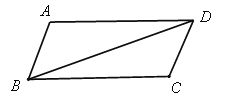
(1)利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法);
(2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE.
参考答案:
【答案】见解析
【解析】解:(1)作图如下:
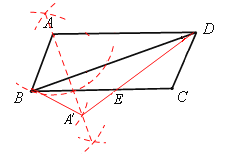
(2)证明:∵四边形ABCD是平行四边形,∴∠A=∠B,AB=DC。
∵△ABD沿对角线BD翻折180°得到△AˊBD,
∴∠Aˊ=∠A,AˊB= AB。∴∠Aˊ=∠B,AˊB= DC。
又∵∠AˊEB=∠DEC,∴△BAˊE≌△DCE(AAS)。
(1)作法:①过点A作BD的垂线;
②以点B 为圆心,AB为半径画弧,交BD的垂线于点Aˊ;
③连接AˊB,AˊD。
则△AˊBD即为所求。
(2)由平行四边形和翻折对称的性质,应用AAS即可证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtΔABC中,∠C=90,AC=4cm,BC=3cm.动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t(单位:秒,0<t<2.5).
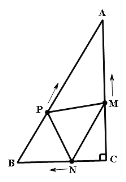
(1)当t为何值时,以A、P、M为顶点的三角形与ΔABC相似?
(2)是否存在某一时刻t,使△PMN 的面积恰好是△ABC 面积的
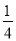 ;若存在求t的值;若不存在,请说明理由.
;若存在求t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH ,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )

A. 12 B. 15 C. 16 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16+(﹣25)+24+(﹣35)
(2)(﹣ )×(﹣1
)×(﹣1  )÷(﹣2
)÷(﹣2  )
)
(3)23×(﹣5)﹣(﹣3)÷
(4)|﹣10|+|(﹣4)2﹣(1﹣32)×2| -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(x﹣4y)(x+4y)+(3x﹣4y)2,其中x=2,y=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=1,BC=
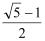 ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.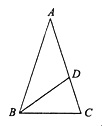
(1)通过计算,判断
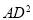 与AC·CD 的大小关系;
与AC·CD 的大小关系;(2)求∠ABD 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.

(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
相关试题

