【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
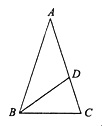
(1)通过计算,判断![]() 与AC·CD 的大小关系;
与AC·CD 的大小关系;
(2)求∠ABD 的度数.
参考答案:
【答案】(1)、![]() ;(2)、36°.
;(2)、36°.
【解析】
试题分析:(1)、通过计算得到![]() =
=![]() ,再计算AC·CD,比较即可得到结论;(2)、由
,再计算AC·CD,比较即可得到结论;(2)、由![]() ,得到
,得到![]() , 即
, 即![]() , 从而得到△ABC∽△BDC, 故有
, 从而得到△ABC∽△BDC, 故有![]() , 从而得到BD=BC=AD,故∠A=∠ABD, ∠ABC=∠C=∠BDC. 设∠A=∠ABD=x,则∠BDC=2x,∠ABC=∠C=∠BDC=2x, 由三角形内角和等于180°, 解得:x=36°, 从而得到结论.
, 从而得到BD=BC=AD,故∠A=∠ABD, ∠ABC=∠C=∠BDC. 设∠A=∠ABD=x,则∠BDC=2x,∠ABC=∠C=∠BDC=2x, 由三角形内角和等于180°, 解得:x=36°, 从而得到结论.
试题解析:(1)、∵AD=BC=![]() , ∴
, ∴![]() =
=![]() =
=![]() . ∵AC=1,
. ∵AC=1,
∴CD=![]() =
=![]() , ∴
, ∴![]() ;
;
(2)、∵![]() , ∴
, ∴![]() , 即
, 即![]() , 又∵∠C=∠C,∴△ABC∽△BDC, ∴
, 又∵∠C=∠C,∴△ABC∽△BDC, ∴![]() , 又∵AB=AC, ∴BD=BC=AD, ∴∠A=∠ABD,∠ABC=∠C=∠BDC. 设∠A=∠ABD=x, 则∠BDC=∠A+∠ABD=2x, ∴∠ABC=∠C=∠BDC=2x, ∴∠A+∠ABC+∠C=x+2x+2x=180°, 解得:x=36°,∴∠ABD=36°.
, 又∵AB=AC, ∴BD=BC=AD, ∴∠A=∠ABD,∠ABC=∠C=∠BDC. 设∠A=∠ABD=x, 则∠BDC=∠A+∠ABD=2x, ∴∠ABC=∠C=∠BDC=2x, ∴∠A+∠ABC+∠C=x+2x+2x=180°, 解得:x=36°,∴∠ABD=36°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16+(﹣25)+24+(﹣35)
(2)(﹣ )×(﹣1
)×(﹣1  )÷(﹣2
)÷(﹣2  )
)
(3)23×(﹣5)﹣(﹣3)÷
(4)|﹣10|+|(﹣4)2﹣(1﹣32)×2| -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△AˊBD.
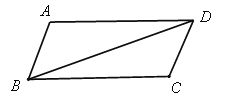
(1)利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法);
(2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(x﹣4y)(x+4y)+(3x﹣4y)2,其中x=2,y=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.

(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组算式中,其值最小的是( )
A. -(-3-2)2 B. (-3)×(-2) C. (-3)2×(-2) D. (-3)÷(-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a、b在数轴上的对应点位置如图所示
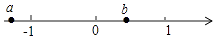
(1)用“<”连接0、﹣a、﹣b、﹣1
(2)化简:|a|﹣2|a+b﹣1|﹣ |b﹣a﹣1|
|b﹣a﹣1|
(3)若a2c+c<0,且c+b>0,求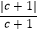 +
+ 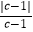 ﹣
﹣ 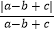 的值.
的值.
相关试题

