【题目】如图,在RtΔABC中,∠C=90,AC=4cm,BC=3cm.动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t(单位:秒,0<t<2.5).
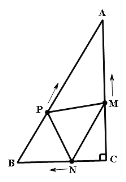
(1)当t为何值时,以A、P、M为顶点的三角形与ΔABC相似?
(2)是否存在某一时刻t,使△PMN 的面积恰好是△ABC 面积的![]() ;若存在求t的值;若不存在,请说明理由.
;若存在求t的值;若不存在,请说明理由.
参考答案:
【答案】(1)、t=![]() ;(2)、t=
;(2)、t=![]()
【解析】
试题分析:(1)、分ΔAMP∽ΔABC和ΔAPM∽ΔABC两种情况讨论;(2)、用t表示出各边长和△PMN 的面积,根据△PMN 的面积恰好是△ABC 面积的![]() 得出一元二次方程,然后解方程即可.
得出一元二次方程,然后解方程即可.
试题解析:(1)、由以A、P、M为顶点的三角形与ΔABC相似,分两种情况:
若ΔAMP∽ΔABC, 则![]() ∴
∴![]()
![]() ∴t=
∴t=![]() ,
,
若ΔAPM∽ΔABC, 则![]() ∴
∴![]() , ∴t=0(不合题意,舍去)
, ∴t=0(不合题意,舍去)
当t=![]() 时,以A、P、M为顶点的三角形与ΔABC相似.
时,以A、P、M为顶点的三角形与ΔABC相似.
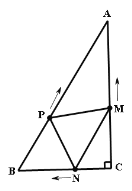
(2)、![]()
![]()
![]() (舍去)
(舍去) ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果2x2y2n-1是七次单项式,则n的值是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+1|=0,b2=9,则a+b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学游戏中,老师在A、B、C三个盘子里分别放了一些糖果,糖果数依次为a0、b0、c0 , 记为G0=(a0 , b0 , c0).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.n次操作后的糖果数记为Gn=(an , bn , cn).小明发现:若G0=(4,8,18),则游戏永远无法结束,那么G2016= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH ,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )

A. 12 B. 15 C. 16 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16+(﹣25)+24+(﹣35)
(2)(﹣ )×(﹣1
)×(﹣1  )÷(﹣2
)÷(﹣2  )
)
(3)23×(﹣5)﹣(﹣3)÷
(4)|﹣10|+|(﹣4)2﹣(1﹣32)×2| -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△AˊBD.
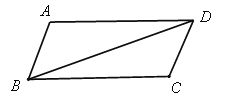
(1)利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法);
(2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE.
相关试题

