【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,以
,以![]() 为一边向外做平行四边形
为一边向外做平行四边形![]() ,连接
,连接![]() ,
,![]() 井延长
井延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,且
,且![]() .
.
(1)如图1,若![]() ,求
,求![]() ;
;

(2)如图1,求证:![]() ;
;
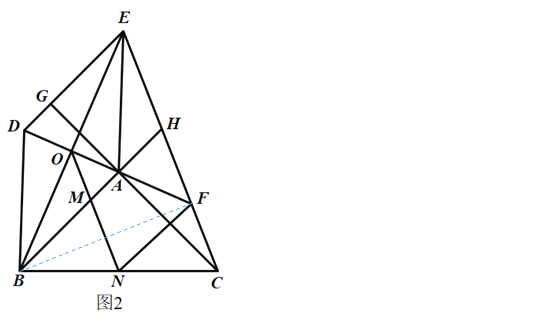
(3)如图2,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,若
,若![]() ,平行四边形
,平行四边形![]() 面积为96,
面积为96,![]() .求
.求![]() 的长.
的长.

参考答案:
【答案】(1)45°;(2)见详解;(3)FN+AN=5![]() +
+![]()
【解析】
(1)首先证明四边形ABDE是菱形,然后利用菱形的性质求出∠EDB的度数,进而求出∠DAG,∠ECB的度数最后利用三角形外角的性质即可求解;
(2)连接BF,由菱形的性质推出△EAF≌△BAF(SAS),根据全等三角形的性质推出∠EFA=∠BFA=45°,进而∠CFB=90°,推出BF2+CF2=BC2,BC2=AB2+AC2=2AB2=2DE2,从而得出BF2+CF2=2DE2
(3)首先通过菱形的面积公式求出BE的长度,进面可求出英形的边长,然后利用三角形中位线的可得出OM,MN.CH的长度,进而利用勾股定理即可求出AH的长度,然后由(2)可知∠BFC=90°,根据中线的性质求得FN=![]() BC=5
BC=5![]() ,则答案可解.
,则答案可解.
解:(1)∵![]() ,
,![]() ,
,
∴AB=BD,
∴平行四边形ABDE是菱形,
∴AB=BD=DE=EA=AC,
∵DE∥AB,∠BAC=90°
∴∠DGA=90°
∵∠EDA=70°
∴∠DAG=180°-∠EDA-∠DGA=180°-70°-90°=20°=∠CAF
∵DE=EA,
∴∠EDA=∠EAD=70°
∴∠GAE=∠EAD-∠CAF=70°-20°=50°
∵EA=AC,
∴∠AEC=∠ACE
∵∠GAE=∠AEC+∠ACE=2∠ACE=50°
∴∠ACE=25°
∴∠EFD=∠ACE +∠CAF=25°+20°=45°
故答案为:∠EFD=45°

(2)证明:如图1,连接BF,
∵平行四边形ABDE是菱形,
∴AE=AB,∴∠EAD=∠BAD=70°
∴∠EAF=∠BAF
在△EAF和△BAF中

∴△EAF≌△BAF(SAS)
∴EF=BF,∠EFA=∠BFA=45°,
∴∠EFB=90°,
∴∠CFB=90°,
∴BF2+CF2=BC2,BC2=AB2+AC2=2AB2=2DE2
∴BF2+CF2=2DE2
(3)如图2,连接BF
∵S菱形ABDE=![]() AD·BE=96,AD=12
AD·BE=96,AD=12
∴BE=16,
∴OE=![]() BE=8,OD=
BE=8,OD=![]() AD=6
AD=6
∴DE=![]()
∴BC=![]()
∵Rt△OEF是等腰直角三角形,
∴EF=2OE,
由(2)结论得,CF=2OD
∴EF=8![]() ,CF=6
,CF=6![]()
∴EF=14![]()
∵O为BE的中点,ON∥EC
∴ON=![]() EC=7
EC=7![]()
∵![]()
∴MN=ON-OM=![]()
∴CH=![]()
∵∠BAC=90°,
∴∠HAC=90°
∴AH=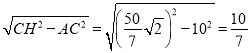
由(2)可知:∠BFC=90°,N是BC的中点,
∴FN=![]() BC=5
BC=5![]() ,
,
∴FN+AN=5![]() +
+![]()
故答案为:FN+AN=5![]() +
+![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
材料1:对于一个关于
 的二次三项式
的二次三项式
 ,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令
,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令
 ,然后移项可得:
,然后移项可得: ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:例:求
 的取值范围:
的取值范围:解:令

∴

∴

∴

∴
 ;
;材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于
 的一元二次方程
的一元二次方程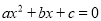 (
( )有两个不相等的实数根
)有两个不相等的实数根 ,
, (
( )
)则关于
 的一元二次不等式
的一元二次不等式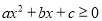 (
( )的解集为:
)的解集为: 或
或 .
.则关于
 的一元二次不等式
的一元二次不等式 (
( )的解集为:
)的解集为: .
.请根据上述材料,解答下列问题:
(1)若关于
 的二次三项式
的二次三项式 (
( 为常数)的最小值为-6,则
为常数)的最小值为-6,则 ________;
________;(2)求出代数式
 的取值范围;
的取值范围;(3)若关于
 的代数式
的代数式 (其中
(其中 、
、 为常数,且
为常数,且 )的最小值为-4,最大值为7,请求出满足条件的
)的最小值为-4,最大值为7,请求出满足条件的 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据
 单位:米
单位:米 ,解答下列问题:
,解答下列问题: 用含m,n的代数式表示地面的总面积S;
用含m,n的代数式表示地面的总面积S; 已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?
已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )

A. △ABC中,AD是边BC上的高
B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高
D. △GBC中,CF是边BG上的高
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为
 ,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形
,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形 的面积是________.
的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2﹣
x2﹣ x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

相关试题

