【题目】阅读理解:
材料1:对于一个关于![]() 的二次三项式
的二次三项式![]()
![]() ,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令
,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令![]()
![]() ,然后移项可得:
,然后移项可得:![]() ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定![]() 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:
例:求![]() 的取值范围:
的取值范围:
解:令![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() )有两个不相等的实数根
)有两个不相等的实数根![]() ,
,![]() (
(![]() )
)
则关于![]() 的一元二次不等式
的一元二次不等式![]() (
(![]() )的解集为:
)的解集为:![]() 或
或![]() .
.
则关于![]() 的一元二次不等式
的一元二次不等式![]() (
(![]() )的解集为:
)的解集为:![]() .
.
请根据上述材料,解答下列问题:
(1)若关于![]() 的二次三项式
的二次三项式![]() (
(![]() 为常数)的最小值为-6,则
为常数)的最小值为-6,则![]() ________;
________;
(2)求出代数式![]() 的取值范围;
的取值范围;
(3)若关于![]() 的代数式
的代数式![]() (其中
(其中![]() 、
、![]() 为常数,且
为常数,且![]() )的最小值为-4,最大值为7,请求出满足条件的
)的最小值为-4,最大值为7,请求出满足条件的![]() ,
,![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() 或
或![]() ,
,![]() .
.
【解析】
(1)根据材料,令![]() ,由根的判别式求出y的取值范围,结合y的最小值即可求出a的值;
,由根的判别式求出y的取值范围,结合y的最小值即可求出a的值;
(2)根据材料,令![]() ,利用根的判别式转化为y的一元二次方程,解不等式即可得到解集;
,利用根的判别式转化为y的一元二次方程,解不等式即可得到解集;
(3)根据材料,令![]() ,利用根的判别式得到y的不等式,然后由根与系数的关系,列出方程组,即可求出
,利用根的判别式得到y的不等式,然后由根与系数的关系,列出方程组,即可求出![]() ,
,![]() 的值.
的值.
解:(1)![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵y的最小值为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
故答案为:![]() ;
;
(2)解:令![]() ,
,
整理得:![]() ,
,
∵方程有解,
![]() ,
,
![]() ,
,
令![]() ,
,
解得![]() ,
,![]() ,
,
![]() 或
或![]() .
.
(3)解:令![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 且
且![]() ,
,
![]() 存在一个
存在一个![]() 使得
使得![]() .
.
当![]() 时,
时,![]() 有解.
有解.
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() 是方程
是方程![]() 的解,
的解,
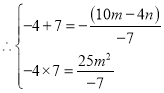 ,
,
解得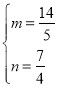 或
或 ,
,
![]() 综上,
综上,![]() ,
,![]() 或
或![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据
 单位:米
单位:米 ,解答下列问题:
,解答下列问题: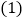 用含m,n的代数式表示地面的总面积S;
用含m,n的代数式表示地面的总面积S;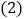 已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?
已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形
 中,
中, ,以
,以 为一边向外做平行四边形
为一边向外做平行四边形 ,连接
,连接 ,
, 井延长
井延长 交
交 于
于 ,延长
,延长 交
交 于
于 ,且
,且 .
.(1)如图1,若
 ,求
,求 ;
;
(2)如图1,求证:
 ;
;(3)如图2,延长
 交
交 于
于 ,连接
,连接 交
交 于
于 ,过
,过 作
作 的平行线交
的平行线交 于
于 ,交
,交 于
于 ,连接
,连接 ,若
,若 ,平行四边形
,平行四边形 面积为96,
面积为96, .求
.求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )

A. △ABC中,AD是边BC上的高
B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高
D. △GBC中,CF是边BG上的高
相关试题

