【题目】如图,抛物线y=![]() x2﹣
x2﹣![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

参考答案:
【答案】(1)AB=9,OC=9;(2)s=![]() m2(0<m<9);(3)
m2(0<m<9);(3)![]() .
.
【解析】试题分析:(1)已知抛物线的解析式,当![]() 可确定
可确定![]() 点坐标;当
点坐标;当![]() 时,可确定
时,可确定![]() 点的坐标,进而确定
点的坐标,进而确定![]() 的长.
的长.
(2)直线![]() 可得出
可得出![]() 相似,它们的面积比等于相似比的平方,由此得到关于
相似,它们的面积比等于相似比的平方,由此得到关于![]() 的函数关系式;根据题干条件:点
的函数关系式;根据题干条件:点![]() 与点
与点![]() 不重合,可确定
不重合,可确定![]() 的取值范围.
的取值范围.
(3)①首先用![]() 列出
列出![]() 的面积表达式,
的面积表达式, ![]() 的面积差即为
的面积差即为![]() 的面积,由此可得关于
的面积,由此可得关于![]() 的函数关系式,根据函数的性质可得到
的函数关系式,根据函数的性质可得到![]() 的最大面积以及此时
的最大面积以及此时![]() 的值;
的值;
②过![]() 做
做![]() 的垂线
的垂线![]() ,这个垂线段的长即为与
,这个垂线段的长即为与![]() 相切的
相切的![]() 的半径,可根据相似三角形
的半径,可根据相似三角形![]() 得到的相关比例线段求得该半径的值,由此得解.
得到的相关比例线段求得该半径的值,由此得解.
试题解析:(1)已知:抛物线![]()
当x=0时,y=9,则:C(0,9);
当y=0时, ![]() ,得:
,得: ![]() ,则:A(3,0)、B(6,0);
,则:A(3,0)、B(6,0);
∴AB=9,OC=9.
(2) ![]()
∴△AED∽△ABC,
 即:
即: 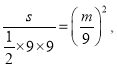 得:
得: ![]()

(3)解法一: ![]()
![]()
∵0<m<9,
∴当![]() 时,
时, ![]() 取得最大值,最大值为
取得最大值,最大值为![]() 此时,
此时, ![]()
记E与BC相切于点M,连接EM,则EM⊥BC,设E的半径为r.
在![]() 中,
中, ![]()
![]()
∴△BOC∽△BME,
![]()

![]()
∴所求![]() 的面积为:
的面积为: 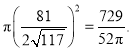
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=
 (x>0)相交于P(1,m).
(x>0)相交于P(1,m).(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,则点Q的坐标为Q( );
(3)若过P、Q两点的抛物线与y轴的交点为N(0,
 ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
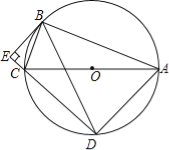
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“龟免赛跑”的故事同学们都非常热悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中_______(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是___________米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来假,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.

-
科目: 来源: 题型:
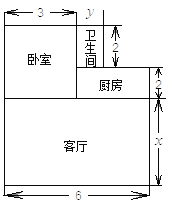
查看答案和解析>>【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含
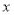 、
、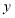 的代数式表示地面总面积;
的代数式表示地面总面积;(2)已知客厅面积比卫生间面积多21平方米,且地面总面积是卫生间面积的15倍.若铺1平方米地砖的平均费用为100元,那么铺地砖的总费用为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12
 D. 16
D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,对于下列结论:①△ABE≌△CDF;②AM=MN=NC;③EM=
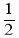 BM,④S△ABM=S△AME,其中正确的有( )
BM,④S△ABM=S△AME,其中正确的有( )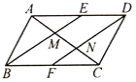
A.1个B.2个C.3个D.4个
相关试题

