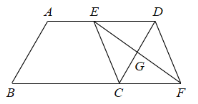
【题目】如图,平行四边形 ABCD 中,AB=8 cm,BC=12 cm,∠B=60°,G 是CD 的中点,E 是边 AD 上的动点,EG 的延长线与 BC 的延长线交于点 F, 连接 CE,DF.
(1)求证:四边形 CEDF 是平行四边形;
(2)①AE= cm 时,四边形 CEDF 是矩形,请写出判定矩形的依据(一条即可);
②AE= cm 时,四边形 CEDF 是菱形,请写出判定菱形的依据(一条即可).
参考答案:
【答案】(1)见解析;(2)①8,有一个角是直角的平行四边形是矩形;②4,有一组邻边相等的平行四边形是菱形
【解析】
(1)先证△EDG≌△FCG,得到ED=FC,根据平行四边形的判定即可得到结论;
(2)①根据有一个角是直角的平行四边形是矩形即可得到结论;
②根据有一组邻边相等的平行四边形是菱形即可得到结论
⑴证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEF=∠EFC,∠CDE=∠DCF.
∵G是CD的中点,
∴DG=CG,
∴△EDG≌△FCG(AAS).
∴ED=FC.
∵ED∥CF,
∴四边形CEDF是平行四边形.
⑵①当AE的值为8时,四边形CEDF是矩形.理由如下:
∵AE=8,AD,
∴ED=4,
∵∠ADC=∠B=60°,ED=DG=4,
∴△EDG为等边三角形,
∴EG=GC,
∴∠DCE=30°
∵∠EDC=60°,
∴∠CDE=90°,
∴平行四边形CEDF是矩形,
故答案为8,有一个角是直角的平行四边形是矩形;
②当AE的值为4时,四边形CEDF是菱形.理由如下:
∵AE=4,
∴ED=8
∴△EDC是等边三角形,
∴ED=EC,
∴平行四边形CEDF是菱形,
故答案为4,有一组邻边相等的平行四边形是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
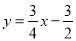 与抛物线
与抛物线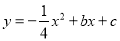 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.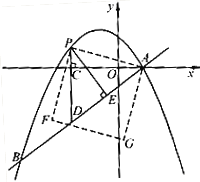
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作如图所示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,求出对应的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F,则下列结论正确的是( )
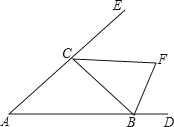
A. 点F在BC边的垂直平分线上 B. 点F在∠BAC的平分线上
C. △BCF是等腰三角形 D. △BCF是直角三角形
-
科目: 来源: 题型:
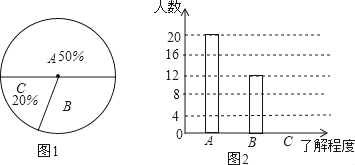
查看答案和解析>>【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)在条形图中,将表示“一般了解”的部分补充完整;
(2)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数为______;
(3)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区活动中心为中老年舞蹈队统一队服和道具,准备购买 10 套某种品牌的舞蹈鞋,每双舞蹈鞋配 x(x≥2)个舞蹈扇,供舞蹈队队员使用.该社区附近 A,B 两家超市都有这种品牌的舞蹈鞋和舞蹈扇出售,且每双舞蹈鞋的标价均为 30 元,每个舞蹈扇的标价为 3 元,目前两家超市同时在做促销活动:
A 超市:所有商品均打九折(按标价的 90%)销售;
B 超市:买一双舞蹈鞋送 2 个舞蹈扇.
设在 A 超市购买舞蹈鞋和舞蹈扇的费用为
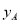 (元),在 B 超市购买舞蹈鞋和舞蹈扇的费用为
(元),在 B 超市购买舞蹈鞋和舞蹈扇的费用为 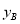 (元).请解答下列问题:
(元).请解答下列问题:(1)分别写出
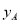 ,
,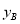 与 x 之间的关系式;
与 x 之间的关系式;(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的边长是
 ,若反比例函数y=
,若反比例函数y= 的图象经过点B,则k的值为_____.
的图象经过点B,则k的值为_____.
相关试题

