【题目】如图,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
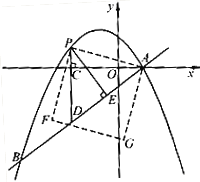
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作如图所示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,求出对应的点P的坐标.
参考答案:
【答案】(1)![]() (2)①15 ②
(2)①15 ②
【解析】试题分析:(1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式解答;(2)①利用直线解析式和抛物线解析式表示出PD,再利用同角的余角相等求出∠DPE=∠BAO,根据直线k值求出∠BAO的正弦和余弦值,然后表示出PE、DE,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答;②分(i)点G在y轴上时,过点P作PH⊥x轴于H,根据正方形的性质可得AP=AG,∠PAG=90°,再求出∠PAH=∠AGO,然后利用“角角边”证明△APH和△GAO全等,根据全等三角形对应边相等可得PH=AO=2,然后利用二次函数解析式求解即可;(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,根据正方形的性质可得AP=FP,∠APF=90°,再根据同角的余角相等求出∠APM=∠FPN,然后利用“角边角”证明△APM和△FPN全等,根据全等三角形对应边相等可得PM=PN,从而得到点P的横坐标与纵坐标相等,再根据二次函数的解析式求解即可.
试题解析:
(1)令y=0,则![]() x﹣
x﹣![]() =0,解得x=2,
=0,解得x=2,
x=﹣8时,y=![]() ×(﹣8)﹣
×(﹣8)﹣![]() =﹣
=﹣![]() ,
,
∴点A(2,0),B(﹣8,﹣![]() ),
),
把点A、B代入抛物线得, ,
,
解得![]() ,
,
所以,该抛物线的解析式![]() ;
;
(2)①∵点P在抛物线上,点D在直线上,
∴PD=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ﹣(
﹣(![]() x﹣
x﹣![]() )=﹣
)=﹣![]() x2﹣
x2﹣![]() x+4,
x+4,
∵PE⊥AB,
∴∠DPE+∠PDE=90°,
又∵PD⊥x轴,
∴∠BAO+∠PDE=90°,
∴∠DPE=∠BAO,
∵直线解析式k=![]() ,
,
∴sin∠BAO=![]() ,cos∠BAO=
,cos∠BAO=![]() ,
,
∴PE=PDcos∠DPE=![]() PD,
PD,
DE=PDsin∠DPE=![]() PD,
PD,
∴△PDE的周长为m=PD+![]() PD+
PD+![]() PD=
PD=![]() PD=
PD=![]() (﹣
(﹣![]() x2﹣
x2﹣![]() x+4)=﹣
x+4)=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,
,
即m=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ;
;
∵m=﹣![]() (x2+6x+9)+15,
(x2+6x+9)+15,
∴当x=﹣3时,最大值为15;
②∵点A(2,0),
∴AO=2,
分(i)点G在y轴上时,过点P作PH⊥x轴于H,
在正方形APFG中,AP=AG,∠PAG=90°,
∵∠PAH+∠OAG=90°,∠AGO+∠OAG=90°,
∴∠PAH=∠AGO,
在△APH和△GAO中,
 ,
,
∴△APH≌△GAO(AAS),

∴PH=AO=2,
∴点P的纵坐标为2,
∴﹣![]() x2﹣
x2﹣![]() x+
x+![]() =2,
=2,
整理得,x2+3x﹣2=0,
解得x=![]() ,
,
∴点P1(![]() ,2),P2(
,2),P2(![]() ,2);
,2);
(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,
在正方形APFG中,AP=FP,∠APF=90°,
∵∠APM+∠MPF=90°,∠FPN+∠MPF=90°,
∴∠APM=∠FPN,
在△APM和△FPN中,
 ,
,
∴△APM≌△FPN(AAS),
∴PM=PN,
∴点P的横坐标与纵坐标相等,
∴﹣![]() x2﹣
x2﹣![]() x+
x+![]() =x,
=x,
整理得,x2+7x﹣10=0,
解得x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
∴点P3(![]() ,
,![]() )
)
综上所述,存在点P1(![]() ,2),P2(
,2),P2(![]() ,2),P3(
,2),P3(![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=2x+2与直线 l2:y2=mx+8相交于点 P(2,b).
(1)求 b,m 的值;
(2)直接写出当 y1<y2 时,自变量 x 的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点在第一象限及x轴、y轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,即(0,0)→(1,0)→(1,1)→)(0,1)→(0,2)→……,且每秒移动一个单位,那么第2018秒时,点所在位置的坐标是( ).

A. (6,44)B. (38,44)C. (44,38)D. (44,6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F,则下列结论正确的是( )
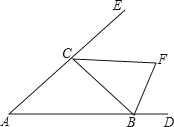
A. 点F在BC边的垂直平分线上 B. 点F在∠BAC的平分线上
C. △BCF是等腰三角形 D. △BCF是直角三角形
-
科目: 来源: 题型:
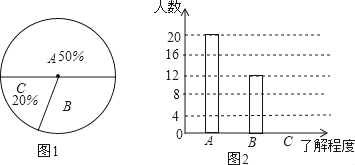
查看答案和解析>>【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)在条形图中,将表示“一般了解”的部分补充完整;
(2)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数为______;
(3)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
-
科目: 来源: 题型:
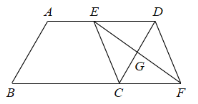
查看答案和解析>>【题目】如图,平行四边形 ABCD 中,AB=8 cm,BC=12 cm,∠B=60°,G 是CD 的中点,E 是边 AD 上的动点,EG 的延长线与 BC 的延长线交于点 F, 连接 CE,DF.
(1)求证:四边形 CEDF 是平行四边形;
(2)①AE= cm 时,四边形 CEDF 是矩形,请写出判定矩形的依据(一条即可);
②AE= cm 时,四边形 CEDF 是菱形,请写出判定菱形的依据(一条即可).
相关试题

