【题目】原题呈现:若a2+b2+4a﹣2b+5=0,求a、b的值.
方法介绍:
①看到a2+4a可想到如果添上常数4恰好就是a2+4a+4=(a+2)2,这个过程叫做“配方”,同理b2﹣2b+1=(b﹣1)2,恰好把常数5分配完;
②从而原式可以化为(a+2)2+(b﹣1)2=0由平方的非负性可得a+2=0且b﹣1=0.
经验运用:
(1)若4a2+b2﹣20a+6b+34=0,求a+b的值.
(2)若a2+5b2+c2﹣2ab﹣4b+6c+10=0,求a+b+c的值.
参考答案:
【答案】(1) -![]() ;(2)-2.
;(2)-2.
【解析】
(1)将已知等式整理,配方,利用偶次方的非负性可求得a和b的值,从而a+b的值可求;
(2)将已知等式整理,配方,利用偶次方的非负性可求得a、b、c的值,从而a+b+c的值可求.
解:(1)已知等式整理得:
4a2-20a+25+b2+6b+9=0,
即(2a-5)2+(b+3)2=0,
∴2a-5=0,b+3=0,
解得:a=![]() ,b=-3,
,b=-3,
∴a+b=-![]() ;
;
(2)已知等式整理得:
![]()
![]()
![]() ,
,
∴![]()
-
科目: 来源: 题型:
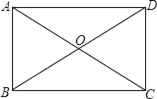
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于点O,△OAB是等边三角形.
(1)求证:ABCD为矩形;
(2)若AB=4,求ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“大美武汉,畅游江城”.某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
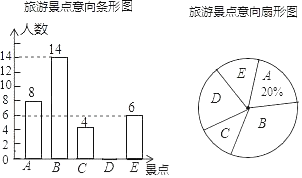
请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有1200名学生,请估计“最想去景点B“的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=﹣
 x+b分别与x轴、y轴交于点A、点B,与直线l2:y2=x交于点C(2,2).
x+b分别与x轴、y轴交于点A、点B,与直线l2:y2=x交于点C(2,2).(1)若y1<y2,请直接写出x的取值范围;
(2)点P在直线l1:y1=﹣
 x+b上,且△OPC的面积为3,求点P的坐标?
x+b上,且△OPC的面积为3,求点P的坐标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线y=
 x+
x+ 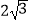 与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0,
与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0, 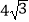 ).
).
(1)求证:OE=CE;
(2)请判断直线CD与⊙P位置关系,证明你的结论,并求出⊙P半径的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
相关试题

