【题目】如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线y= ![]() x+
x+ ![]() 与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0,
与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0, ![]() ).
).
(1)求证:OE=CE;
(2)请判断直线CD与⊙P位置关系,证明你的结论,并求出⊙P半径的值.
参考答案:
【答案】
(1)证明:如图所示,连接OC,

∵直线y= ![]() x+
x+ ![]() 与y轴相交于点E,
与y轴相交于点E,
∴点E的坐标为(0, ![]() ),即OE=
),即OE= ![]() .
.
又∵点B的坐标为(0, ![]() ),
),
∴OB= ![]() ,
,
∴BE=OE= ![]() ,
,
又∵OA是⊙P的直径,
∴∠ACO=90°,即OC⊥AB,
∴OE=CE.
(2)直线CD是⊙P的切线.
证明:连接PC,PE,由(1)可知OE=CE.
在△POE和△PCE中, 
∴△POE≌△PCE,
∴∠POE=∠PCE.
又∵x轴⊥y轴,
∴∠POE=∠PCE=90°,
∴PC⊥CE,即PC⊥CD.
又∵直线CD经过半径PC的外端点C,
∴直线CD是⊙P的切线.
∵对y= ![]() x+
x+ ![]() ,当y=0时,x=-6,即OD=6,
,当y=0时,x=-6,即OD=6,
在Rt△DOE中,DE= ![]() =
= ![]() =
= ![]() ,
,
∴CD=DE+EC=DE+OE= ![]() +
+ ![]() =
= ![]() .
.
设⊙P的半径为r,
则在Rt△PCD中,由勾股定理知PC2+CD2=PD2,
即r2+(6 ![]() )2=(6+r)2,
)2=(6+r)2,
解得r=6,即⊙P半径的值为6.
【解析】(1)连接OC,利用已知条件计算出CE和OB的长度,再证明△BCO为直角三角形,利用:直角三角形斜边上的中线等于斜边的一半即可证明OE=CE。
(2)①要证直线CD是⊙P的切线,需证明PC⊥CD,先证明△POE≌△PCE,得出∠POE=∠PCE,再根据∠POE是直角,证明PC⊥CD即可得出结论;
②设⊙P的半径为r,则在Rt△PCD中,由勾股定理得到关于r的方程,求出r即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】原题呈现:若a2+b2+4a﹣2b+5=0,求a、b的值.
方法介绍:
①看到a2+4a可想到如果添上常数4恰好就是a2+4a+4=(a+2)2,这个过程叫做“配方”,同理b2﹣2b+1=(b﹣1)2,恰好把常数5分配完;
②从而原式可以化为(a+2)2+(b﹣1)2=0由平方的非负性可得a+2=0且b﹣1=0.
经验运用:
(1)若4a2+b2﹣20a+6b+34=0,求a+b的值.
(2)若a2+5b2+c2﹣2ab﹣4b+6c+10=0,求a+b+c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=﹣
 x+b分别与x轴、y轴交于点A、点B,与直线l2:y2=x交于点C(2,2).
x+b分别与x轴、y轴交于点A、点B,与直线l2:y2=x交于点C(2,2).(1)若y1<y2,请直接写出x的取值范围;
(2)点P在直线l1:y1=﹣
 x+b上,且△OPC的面积为3,求点P的坐标?
x+b上,且△OPC的面积为3,求点P的坐标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,
 ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由. -
科目: 来源: 题型:
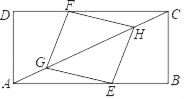
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
相关试题

