【题目】已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)

参考答案:
【答案】![]() (α+β).
(α+β).
【解析】
连接BC,根据角平分线的性质得到∠3=![]() ∠ABP,∠4=
∠ABP,∠4=![]() ∠ACP,根据三角形的内角和得到∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,求出∠3+∠4=
∠ACP,根据三角形的内角和得到∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,求出∠3+∠4=![]() (β-α),根据三角形的内角和即可得到结论.
(β-α),根据三角形的内角和即可得到结论.
解:连接BC,
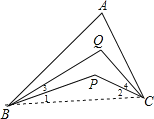
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=![]() ∠ABP,∠4=
∠ABP,∠4=![]() ∠ACP,
∠ACP,
∵∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,
∴∠3+∠4=![]() (β-α),
(β-α),
∵∠BQC=180°-(∠1+∠2)-(∠3+∠4)=180°-(180°-β)-![]() (β-α),
(β-α),
即:∠BQC=![]() (α+β).
(α+β).
故答案为:![]() (α+β).
(α+β).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=
 ∠CAB,∠CDP=
∠CAB,∠CDP= ∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
-
科目: 来源: 题型:
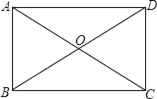
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于点O,△OAB是等边三角形.
(1)求证:ABCD为矩形;
(2)若AB=4,求ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“大美武汉,畅游江城”.某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
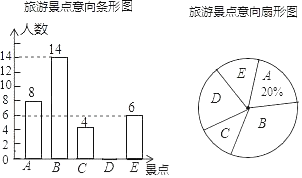
请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有1200名学生,请估计“最想去景点B“的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】原题呈现:若a2+b2+4a﹣2b+5=0,求a、b的值.
方法介绍:
①看到a2+4a可想到如果添上常数4恰好就是a2+4a+4=(a+2)2,这个过程叫做“配方”,同理b2﹣2b+1=(b﹣1)2,恰好把常数5分配完;
②从而原式可以化为(a+2)2+(b﹣1)2=0由平方的非负性可得a+2=0且b﹣1=0.
经验运用:
(1)若4a2+b2﹣20a+6b+34=0,求a+b的值.
(2)若a2+5b2+c2﹣2ab﹣4b+6c+10=0,求a+b+c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=﹣
 x+b分别与x轴、y轴交于点A、点B,与直线l2:y2=x交于点C(2,2).
x+b分别与x轴、y轴交于点A、点B,与直线l2:y2=x交于点C(2,2).(1)若y1<y2,请直接写出x的取值范围;
(2)点P在直线l1:y1=﹣
 x+b上,且△OPC的面积为3,求点P的坐标?
x+b上,且△OPC的面积为3,求点P的坐标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线y=
 x+
x+ 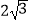 与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0,
与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0, 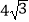 ).
).
(1)求证:OE=CE;
(2)请判断直线CD与⊙P位置关系,证明你的结论,并求出⊙P半径的值.
相关试题

