【题目】已知二次函数 ![]() (
( ![]() 是常数).
是常数).
(1)求证:不论 ![]() 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿 ![]() 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与 ![]() 轴只有一个公共点?
轴只有一个公共点?
参考答案:
【答案】
(1)解:∵△=(﹣2m)2﹣4×1×(m2+3)=4m2﹣4m2﹣12=﹣12<0
∴方程x2﹣2mx+m2+3=0没有实数解, 即不论m为何值,该函数的图象与x轴没有公共点;
(2)解:y=x2﹣2mx+m2+3=(x﹣m)2+3,
∴把函数y=x2﹣2mx+m2+3的图象沿y轴向下平移3个单位长度后,得到的函数的图象与x轴只有一个公共点.
【解析】(1)根据△=b2-4ac>0方程有两个不相等的两个实数根,△=0,方程有两个相等的实数根,△<0,方程没有实数根;由△=(﹣2m)2﹣4×1×(m2+3)=4m2﹣4m2﹣12=﹣12<0,得到方程x2﹣2mx+m2+3=0没有实数解, 即不论m为何值,该函数的图象与x轴没有公共点;(2)根据顶点式得到把函数的图象沿y轴向下平移3个单位长度后,得到的函数的图象与x轴只有一个公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.

(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3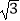 ,AE=3,求AF的长.
,AE=3,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理填空:如图,已知 AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.

解:因为 AB∥CD(已知),
所以∠AGF+ =180°( ),
因为 GH 平分∠AGF,MN 平分∠CMG( ),
所以∠1=
 ∠AGF,∠2=
∠AGF,∠2=  ∠CMG( ),
∠CMG( ), 得∠1+∠2=
 (∠AGF+∠CMG)= ,
(∠AGF+∠CMG)= , 所以 GH⊥MN( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
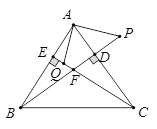
求证:(1)AP=AQ ;
(2)AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度
 ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在
 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的  处飞出(
处飞出(  在
在  轴上),运动员孙可在距
轴上),运动员孙可在距  点6米的
点6米的  处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点  ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 距守门员多少米?(取
距守门员多少米?(取  )
)
(3)孙可要抢到足球第二个落地点 ,他应从第一次落地点
,他应从第一次落地点  再向前跑多少米?(取
再向前跑多少米?(取  )
) -
科目: 来源: 题型:
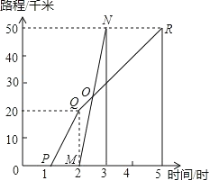
查看答案和解析>>【题目】如图所示 A、B 两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地.如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
(1)甲乙两人中, 先出发,先出发 小时.
(2)甲乙两人中, 先到达B地,先到 小时.
(3)分别求出乙骑摩托车的速度和甲骑自行车在全程的平均速度.
(4)乙出发大约用多长时间就追上甲?
相关试题

