【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
参考答案:
【答案】
(1)解:∵四边形ABCD是平行四边形
∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180°
∵∠AFE+∠AFD=180° ∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形
∴AD∥BC CD=AB=4
又∵AE⊥BC
∴ AE⊥AD
在Rt△ADE中,DE= ![]()
∵△ADF∽△DEC
∴ ![]()
∴ ![]()
AF= ![]()
【解析】(1)根据平行四边形的性质,求出∠ADF=∠CED 、∠AFD=∠C ,根据两角相等两三角形相似,得到△ADF∽△DEC;(2)在Rt△ADE中,根据勾股定理求出DE的值,由(1)中的△ADF∽△DEC,得到比例,求出AF的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式的乘法中,可以用平方差公式计算的有( )
A.(x+
 )(﹣x﹣
)(﹣x﹣ )B.(﹣2+m)(﹣m﹣2)
)B.(﹣2+m)(﹣m﹣2)C.(﹣a+b)(a﹣b)D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_______cm/s时,能够使△BPE≌△CQP.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理填空:如图,已知 AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.

解:因为 AB∥CD(已知),
所以∠AGF+ =180°( ),
因为 GH 平分∠AGF,MN 平分∠CMG( ),
所以∠1=
 ∠AGF,∠2=
∠AGF,∠2=  ∠CMG( ),
∠CMG( ), 得∠1+∠2=
 (∠AGF+∠CMG)= ,
(∠AGF+∠CMG)= , 所以 GH⊥MN( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
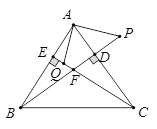
求证:(1)AP=AQ ;
(2)AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 (
(  是常数).
是常数).
(1)求证:不论 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与 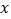 轴只有一个公共点?
轴只有一个公共点?
相关试题

