Question

【题目】如图（1），在△ABC中，∠C=90°，AB=5cm，BC=3cm，动点P在线段AC上以5cm/s的速度从点A运动到点C，过点P作PD⊥AB于点D，将△APD绕PD的中点旋转180°得到△A′DP，设点P的运动时间为x（s）．

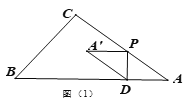
（1）PD=_________、AD=_________；（用x的代数式表示）

（2）当点A′落在边BC上时，求x的值．

（3）如图（2），另有一动点Q与点P同时出发，在线段BC上以5cm/s的速度从点B运动到点C，过点Q作QE⊥AB于点E，将△BQE绕QE的中点旋转180°得到△B′EQ，

①连结A′B′，当直线A′B′与△ABC的一边垂直时，求线段A′B′的长．

②当A′关于QE的对称点落在四边形BE B′Q的内部（包括边上）时，直接写出x的取值范围．

Answer 1

【答案】 3x 4x

【解析】试题分析：（1）由勾股定理和相似三角形的判定与性质即可表示出PD、AD的值；

（2）当A’在BC边上时，根据线段之间的数量关系，求出x的值；

（3）分A′B′⊥AB时，A′B′⊥BC时，A′B′⊥AC时，结合锐角三角函数的概念，即可求得A'B'的长度．

试题解析： (1)PD=3x,AD=4x；

(2)如图（1）当点A′落在边BC上时，由题意得

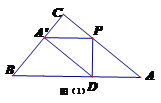
四边形AP A′D为平行四边形

∵△APD∽△ABC，AP=5x，

∴ A′P=AD=4x，PC=4－5x．∵A′P//AB ∴△A′PC∽△ABC．

x＝．当点A′落在边BC上时， x＝．

(3) Ⅰ、当A′B′⊥AB时，如图6，

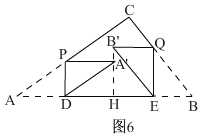
∴DH=PA′=AD,HE=B′Q=EB，

∵AB=2AD+2EB=2×4x+2×3x=5，

∴x=，

∴A′B′=QEPD=x=；

Ⅱ、当A′B′⊥BC时，如图7，

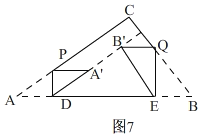
∴B′E=5x，DE=57x，

∴cosB==35，

∴x=，

∴A′B′=B′DA′D=；

Ⅲ、当A′B′⊥AC时，如图8，

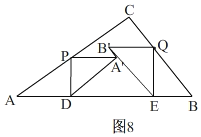
由(1)有,x=，

∴A′B′=PA′sinA=；

当A′B′⊥AB时,x=,A1B1=．

当A′B′⊥BC时x=, A1B1=．

当A′B′⊥AC时x=, A1B1=．

②.

点睛（1）根据勾股定理求出AC，证明△APD∽△ABC，根据相似三角形的性质计算；

（2）根据四边形AP A′D为平行四边形，△APD∽△ABC， A′PC∽△ABC进行解答；

（3）根据题意画出图形，分三种情况，结合锐角三角函数的概念计算．