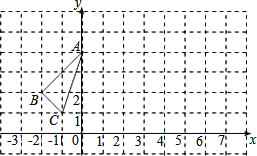
【题目】如图,已知在平面直角坐标系中,三角形ABC的位置如图所示.
(1)请写出A、B、C三点的坐标;
(2)求△ABC的面积;
(3)△ABC经过平移后得到△A′B′C′,已知△ABC内的任意一点P(x,y)在△A′B′C′内的对应点P′的坐标为(x+6,y+2).请你写出△A′B′C′各顶点的坐标并图中画出△A′B′C′.
参考答案:
【答案】(1)点A的坐标为(0,4),点B的坐标为(﹣2,2),点C的坐标为(﹣1,1);(2)S△ABC=2;(3)A'坐标为(6,6),点B'的坐标为(4,4),点C'的坐标为(5,3);作出图形如图所示,见解析.
【解析】
(1)结合直角坐标系,即可得出A、B、C三点的坐标;
(2)根据图形可判断△ABC为直角三角形,∠ABC=90°,代入直角三角形的面积公式进行计算即可.
(3)平移是按照:向右平移6个单位,向上平移2个单位进行,从而可得出△A′B′C′各顶点的坐标,可也画出图形.
(1)结合图形可得:点A的坐标为(0,4),点B的坐标为(﹣2,2),点C的坐标为(﹣1,1);
(2)由图形可得∠ABC=90°,
则S△ABC=![]() AB×BC=
AB×BC=![]() ×2
×2![]() ×
×![]() =2;
=2;
(3)由点P平移前后的坐标可得:平移是按照:向右平移6个单位,向上平移2个单位进行的,
则A'坐标为(6,6),点B'的坐标为(4,4),点C'的坐标为(5,3);
作出图形如下所示:
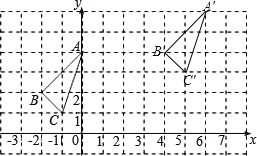 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列三个结论:
①∠BOC=90°+
 ∠A;②设OD=m,AE+AF=n,则S△AEF=mn;③EF是△ABC的中位线.其中正确的结论是________.
∠A;②设OD=m,AE+AF=n,则S△AEF=mn;③EF是△ABC的中位线.其中正确的结论是________.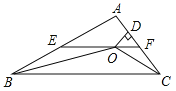
-
科目: 来源: 题型:
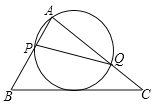
查看答案和解析>>【题目】如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点
 (-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )
(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )A. (-3,3) B. (-2,-2) C. (3,-1) D. (2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,初中学生课桌椅不合格率达76.7%(不合格是指不能按照学生不同的身高来调节课桌椅的高度),为了解初中生的身高情况,随机抽取了某校初中部分男生、女生进行调查收集数据如下:
男生身高(单位:cm):163 161 160 163 161 162 163 164 163 163
女生身高(单位:cm):164 161 160 161 161 162 160 162 163 162
整理数据:
160
161
162
163
164
男生(人)
1
2
1
a
1
女生(人)
2
b
3
1
1
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)现有两名身高都为163cm的男生和女生,比较这两名同学分别在男生、女生中的身高情况,并简述理由;
(3)根据相关研究发现,只有身高为161cm的初中生课桌椅是合格的,试估计全校1000名学生中,有多少名学生的课桌椅是合格的?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
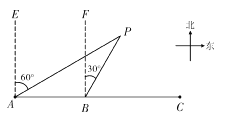
查看答案和解析>>【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:
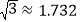 )
)
相关试题

