【题目】如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于_______________.
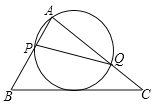
参考答案:
【答案】![]()
【解析】如图,设点O是△APQ的外接圆的圆心,连接OP,OQ,作OH⊥PQ于点H,过点A作AD⊥BC于点D,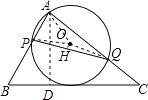
∴PH=QH=![]() PQ,
PQ,
∵OP=OQ,
∴∠POH=![]() ∠POQ,
∠POQ,
∵∠POQ=2∠BAC,
∴∠POH=∠BAC,
在Rt△POH中,PH=OPsin∠POH=OAsin∠BAC,
∴PQ=2OAsin∠BAC,
即当OA最小时,PQ最小,
∵当AD是直径时,即OA=![]() AD时,PQ最小,
AD时,PQ最小,
设BD=x,则CD=8-x,
∵在Rt△ABD中,AD2=AB2-AD2,
在Rt△ACD中,AD2=AC2-CD2,
∴25-x2=49-(8-x)2,
解得:x=![]() ,
,
∴AD=![]() =
=![]() ,
,
∴OA=![]() ,
,
设AC边上的高为h,
则ACh=BCAD,
∴h=![]() ,
,
∴sin∠BAC=![]() =
=![]() ,
,
∴PQ=2OAsin∠BAC=2×![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
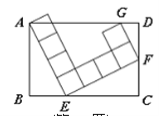
查看答案和解析>>【题目】如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为 _ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四个三角形,分别满足下列条件:(1)一个角等于另外两个内角之和;(2)三个内角之比为3:4:5;(3)三边之比为5:12:13;(4)三边长分别为5,24,25.其中直角三角形有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列三个结论:
①∠BOC=90°+
 ∠A;②设OD=m,AE+AF=n,则S△AEF=mn;③EF是△ABC的中位线.其中正确的结论是________.
∠A;②设OD=m,AE+AF=n,则S△AEF=mn;③EF是△ABC的中位线.其中正确的结论是________.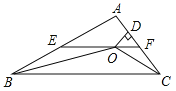
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点
 (-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )
(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )A. (-3,3) B. (-2,-2) C. (3,-1) D. (2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,三角形ABC的位置如图所示.
(1)请写出A、B、C三点的坐标;
(2)求△ABC的面积;
(3)△ABC经过平移后得到△A′B′C′,已知△ABC内的任意一点P(x,y)在△A′B′C′内的对应点P′的坐标为(x+6,y+2).请你写出△A′B′C′各顶点的坐标并图中画出△A′B′C′.
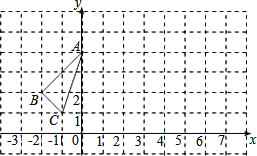
-
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,初中学生课桌椅不合格率达76.7%(不合格是指不能按照学生不同的身高来调节课桌椅的高度),为了解初中生的身高情况,随机抽取了某校初中部分男生、女生进行调查收集数据如下:
男生身高(单位:cm):163 161 160 163 161 162 163 164 163 163
女生身高(单位:cm):164 161 160 161 161 162 160 162 163 162
整理数据:
160
161
162
163
164
男生(人)
1
2
1
a
1
女生(人)
2
b
3
1
1
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)现有两名身高都为163cm的男生和女生,比较这两名同学分别在男生、女生中的身高情况,并简述理由;
(3)根据相关研究发现,只有身高为161cm的初中生课桌椅是合格的,试估计全校1000名学生中,有多少名学生的课桌椅是合格的?

相关试题

