【题目】如图,矩形OABC中,A(6,0)、C(0,2![]() )、D(0,3
)、D(0,3![]() ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
(1)①点B的坐标是 ;②∠CAO= 度;③当点Q与点A重合 时,点P的坐标为 ;(直接写出答案)
(2)设OA的中点为N,PQ与线段AC相交于点M,是否存在点P,使△AMN为等腰三角形?若存在,请直接写出点P的横坐标为m;若不存在,请说明理由.
(3)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.

参考答案:
【答案】(1)①(6,2![]() ),②30,③(3,3
),②30,③(3,3![]() );(2)m=0或m=3-
);(2)m=0或m=3-![]() 或m=2;(3)当0≤x≤3时,S梯形=
或m=2;(3)当0≤x≤3时,S梯形=![]() (3+x);当3<x≤5时,S=
(3+x);当3<x≤5时,S=![]() (3+x)-
(3+x)-![]() (x-3)2;当5<x≤9时,S=
(x-3)2;当5<x≤9时,S=![]() (12-
(12-![]() x);当9<x时,S=
x);当9<x时,S=![]() .
.
【解析】矩形的性质,梯形的性质,锐角三角函数,特殊角的三角函数值,相似三角形的判定和性质,解直角三角形。
(1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标:
∵四边形OABC是矩形,∴AB=OC,OA=BC,
∵A(6,0)、C(0,2![]() ),∴点B的坐标为:(6,2
),∴点B的坐标为:(6,2![]() )。
)。
②由正切函数,即可求得∠CAO的度数:
∵![]() ,∴∠CAO=30°。
,∴∠CAO=30°。
③由三角函数的性质,即可求得点P的坐标;如图:当点Q与点A重合时,过点P作PE⊥OA于E,
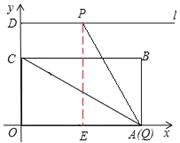
∵∠PQO=60°,D(0,3![]() ),∴PE=3
),∴PE=3![]() 。
。
∴![]() 。
。
∴OE=OA﹣AE=6﹣3=3,∴点P的坐标为(3,3![]() )。
)。
(2)分别从MN=AN,AM=AN与AM=MN去分析求解即可求得答案:
情况①:
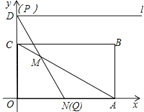
MN=AN=3,则∠AMN=∠MAN=30°,
∴∠MNO=60°。
∵∠PQO=60°,即∠MQO=60°,∴点N与Q重合。
∴点P与D重合。∴此时m=0。
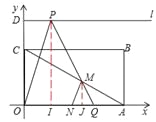
情况②,如图AM=AN,作MJ⊥x轴、PI⊥x轴。
MJ=MQsin60°=AQsin600
![]()
又![]() ,
,
∴![]() ,解得:m=3﹣
,解得:m=3﹣![]() 。
。
情况③AM=NM,此时M的横坐标是4.5,
过点P作PK⊥OA于K,过点M作MG⊥OA于G,
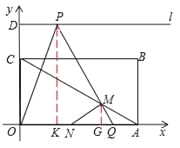
∴MG=![]() 。
。
∴![]() 。
。
∴KG=3﹣0.5=2.5,AG=![]() AN=1.5。∴OK=2。∴m=2。
AN=1.5。∴OK=2。∴m=2。
综上所述,点P的横坐标为m=0或m=3﹣![]() 或m=2。
或m=2。
(3)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一棵树高h(m)与生长时间n(年)之间有一定关系,请你根据下表中数据,写出h(m)与n(年)之间的关系式:_____.
n/年
2
4
6
8
…
h/m
2.6
3.2
3.8
4.4
…
-
科目: 来源: 题型:
查看答案和解析>>【题目】一根弹簧的长度为10厘米,当弹簧受到
 千克的拉力时(
千克的拉力时( 不超过10),弹簧的长度是
不超过10),弹簧的长度是 (厘米),测得有关数据如下表所示:
(厘米),测得有关数据如下表所示:拉力
 (千克)
(千克)1
2
3
4
…
弹簧的长度
 (厘米)
(厘米)



…
(1)写出弹簧长度
 (厘米)关于拉力
(厘米)关于拉力 (千克)的函数解析式;
(千克)的函数解析式;(2)如果拉力是10千克,那么弹簧长度是多少厘米?
(3)当拉力是多少时,弹簧长度是14厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1使它与△ABC的相似比为2;则点B的对应点B1的坐标是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店零售一种商品,其质量x(kg)与售价y(元)之间的关系如下表:
x/kg
1
2
3
4
5
6
7
8
y/元
2.4
4.8
7.2
9.6
12
14.4
16.8
19.2
根据销售经验可知,在此处零买这种商品的顾客所买商品均未超过8kg.
(1)由上表推出售价y(元)关于质量x(kg)的函数解析式,并画出函数的图象;
(2)李大婶购买这种商品5.5kg,应付多少元钱.
-
科目: 来源: 题型:
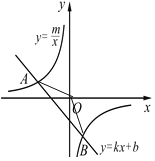
查看答案和解析>>【题目】如图,已知A(-4,2)、B(n,-4)是一次函数
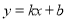 的图象与反比例函数
的图象与反比例函数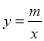 的图象的两个交点.
的图象的两个交点.(1)求此反比例函数和一次函数的解析式;
(2)求△AOB的面积;
相关试题

