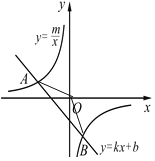
【题目】如图,已知A(-4,2)、B(n,-4)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)求△AOB的面积;
参考答案:
【答案】(1)y=-![]() ;y=-x-2;(2)6
;y=-x-2;(2)6
【解析】试题分析:
(1)先把点A(-4,2)代入![]() ,求得“m”的值得到反比例函数的解析式,再把点B(n,-4)代入所得的反比例函数的解析式中求得“n”的值,从而可得点B的坐标,最后把A、B的坐标代入
,求得“m”的值得到反比例函数的解析式,再把点B(n,-4)代入所得的反比例函数的解析式中求得“n”的值,从而可得点B的坐标,最后把A、B的坐标代入![]() 中列方程组解得“k、b”的值即可得到一次函数的解析式;
中列方程组解得“k、b”的值即可得到一次函数的解析式;
(2)设直线AB和x轴交于点C,先求出点C的坐标,再由S△AOB=S△AOC+S△BOC,即可计算出△AOB的面积;
试题解析:
(1)把点A(-4,2)代入![]() 得:
得: ![]() ,解得:
,解得: ![]() ,
,
∴反比例函数的解析式为: ![]() .
.
把点B(n,-4)代入![]() 得:
得: ![]() ,解得:
,解得: ![]() ,
,
∴点B的坐标为(2,-4).
把点A、B的坐标代入![]() 得:
得: ![]() ,解得
,解得![]() ,
,
∴一次函数的解析式是![]() ;
;
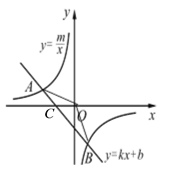
(2)如图,设AB与x轴的交点为点C,
在![]() 中由
中由![]() 可得:
可得: ![]() ,解得:
,解得: ![]() .
.
∴点C的坐标是(-2,0).
∴OC=2,
∴S△AOB=S△AOC+S△BOC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC中,A(6,0)、C(0,2
 )、D(0,3
)、D(0,3 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.(1)①点B的坐标是 ;②∠CAO= 度;③当点Q与点A重合 时,点P的坐标为 ;(直接写出答案)
(2)设OA的中点为N,PQ与线段AC相交于点M,是否存在点P,使△AMN为等腰三角形?若存在,请直接写出点P的横坐标为m;若不存在,请说明理由.
(3)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1使它与△ABC的相似比为2;则点B的对应点B1的坐标是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店零售一种商品,其质量x(kg)与售价y(元)之间的关系如下表:
x/kg
1
2
3
4
5
6
7
8
y/元
2.4
4.8
7.2
9.6
12
14.4
16.8
19.2
根据销售经验可知,在此处零买这种商品的顾客所买商品均未超过8kg.
(1)由上表推出售价y(元)关于质量x(kg)的函数解析式,并画出函数的图象;
(2)李大婶购买这种商品5.5kg,应付多少元钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同,小明先从盒子里随机取出一个小球,记下数字为x,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树形图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在二次函数y=x2的图象上的概率.
-
科目: 来源: 题型:
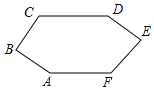
查看答案和解析>>【题目】如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.
(1)观察直线AB与直线DE的位置关系,你能得出什么结论并说明理由.
(2)求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它表示甲乙两人从同一个地点出发后的情况.根据图像判断,下列说法错误的是()

A. 甲是 8 点出发的
B. 乙是 9 点出发的,到 10 点时,他大约走了 10 千米
C. 到 10 点为止,乙的速度快
D. 两人在 12 点再次相遇
相关试题

