Question

【题目】如图，分别位于反比例函数y＝，y＝在第一象限图象上的两点A，B，与原点O在同一直线上，且.

(1)求反比例函数y＝的表达式；

(2)过点A作x轴的平行线交y＝的图象于点C，连接BC，求△ABC的面积．

Answer 1

【答案】(1)y＝；(2) 8.

【解析】试题分析：（1）作AE、BF分别垂直于x轴，垂足为E、F，根据△AOE∽△BOF，则设A的横坐标是m，则可利用m表示出A和B的坐标，利用待定系数法求得k的值；

（2）根据AC∥x轴，则可利用m表示出C的坐标，利用三角形的面积公式求解．

试题解析：

(1)作AE，BF分别垂直于x轴，垂足为E，F，

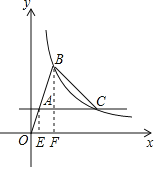
∴AE∥BF，∴△AOE∽△BOF，

∴＝＝＝.

由点A在函数y＝的图象上，

设A的坐标是，

∴＝＝， ＝＝，

∴OF＝3m，BF＝，

即B的坐标是.

又点B在y＝的图象上，

∴＝，解得k＝9，

则反比例函数y＝的表达式是y＝.

(2)由(1)可知A，B，

又已知过A作x轴的平行线交y＝的图象于点C，

∴C的纵坐标是.

把y＝代入y＝得x＝9m，

∴C的坐标是，

∴AC＝9m－m＝8m.

∴S△ABC＝×8m×＝8.