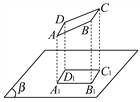
【题目】已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
参考答案:
【答案】50![]() 平方厘米.
平方厘米.
【解析】试题分析:如图所示,过A作AH⊥BB1于H,由∠ABB1=45°可得△ABH是等腰直角三角形,结合cos45°可求出AH的长度,即求出A1B1的长度,又因为A1D1=AD,求出矩形A1B1C1D1的面积即可.
试题解析:
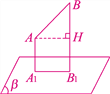
如图所示,过A作AH⊥BB1于H,
∵∠ABB1=45°,
∴△ABH是等腰直角三角形,
∴AH=AB·cos45°=10×![]() =5
=5![]() (厘米),
(厘米),
∴A1B1=AH=5![]() (厘米),
(厘米),
∵A1D1=AD=10(厘米),
∴矩形A1B1C1D1的面积=A1B1·A1D1=5![]() ×10=50
×10=50![]() (平方厘米).
(平方厘米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:(1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB
___A1B1;
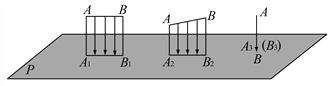
(2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB___A2B2;
(3)当线段AB垂直于投影面P时,它的正投影是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为
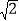 ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )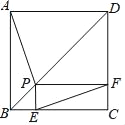
A. ①②③B. ①②④C. ②③④D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
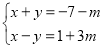 的解满足x为非正数,y为负数.
的解满足x为非正数,y为负数.(1)求m的取值范围;
(2)化简:|m﹣3|﹣|m+2|;
(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
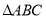 中,
中,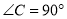 ,
, ,
,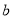 ,
,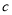 分别是
分别是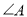 ,
,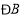 ,
,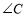 的对边,点
的对边,点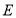 是
是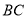 上一个动点(点
上一个动点(点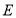 与
与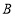 、
、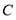 不重合),连
不重合),连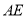 ,若
,若 、
、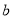 满足
满足 ,且
,且 是不等式组
是不等式组 的最大整数解.
的最大整数解.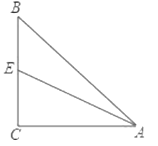
(1)求
 ,
, ,
, 的长;
的长;(2)若
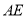 平分
平分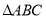 的周长,求
的周长,求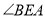 的大小;
的大小;(3)是否存在线段
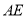 将三角形
将三角形 的周长和面积同时平分?若存在,求出
的周长和面积同时平分?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×5网格图中,其中每个小正方形边长均为1,梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点.
(1)以B为位似中心,在网格图中作四边形A′BC′D′,使四边形A′BC′D′和梯形ABCD位似,且位似比为2:1;
(2)求(1)中四边形A′BC′D′与五边形EFGHK重叠部分的周长.(结果保留根号)

-
科目: 来源: 题型:
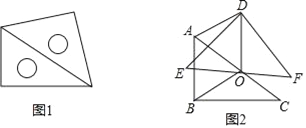
查看答案和解析>>【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD.
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
相关试题

