【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
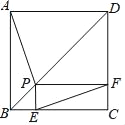
A. ①②③B. ①②④C. ②③④D. ①③④
参考答案:
【答案】A
【解析】
连接PC,可证得△ABP≌△CBP,结合矩形的性质,可证得PA=EF,国判断①;延长AP交BC于点G,可证得AP⊥EF,可判断②;求得AP的最小值即可求得EF的最短长度,可判断③;当点P在点B或点D时,AP有最大值2,则可判断④;可求得答案.
解:
①如图,连接PC,
∵四边形ABCD为正方形,
∴AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中
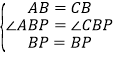
∴△ABP≌△CBP(SAS),
∴AP=PC,
∵PE⊥BC,PF⊥CD,且∠FCE=90°,
∴四边形PECF为矩形,
∴PC=EF,
∴AP=EF,故①正确;
②延长AP交BC于点G,
由①可得∠PCE=∠PFE=∠BAP,
∵PE∥AB,
∴∠EPG=∠BAP,
∴∠EPG=∠PFE,
∵∠EPF=90°,
∴∠EPG+∠PEF=∠PEG+∠PFE=90°,
∴AP⊥EF,故②正确;
③当AP⊥BD时,AP有最小值![]() ,此时P为BD的中点,
,此时P为BD的中点,
由①可知EF=AP,
∴EF的最短长度为![]() ,故③正确;
,故③正确;
④当点P在点B或点D位置时,AP=AB=2,
∴EF=AP≤2,
∴当∠BAP=30°时,AP<2,
即EF的长度不可能为2,故④不正确;
综上可知正确的结论为①②③,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于
 BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )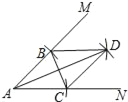
A. AD平分∠MAN B. AD垂直平分BC
C. ∠MBD=∠NCD D. 四边形ACDB一定是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
(1)当m=
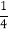 时,n=_____;
时,n=_____;(2)随着点M的转动,当m从
 变化到
变化到 时,点N相应移动的路径长为_____.
时,点N相应移动的路径长为_____.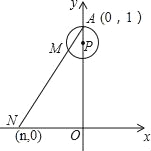
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB:y=﹣
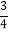 x+
x+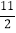 与直线AC:y=
与直线AC:y=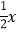 +8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.
+8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.(1)求点A的坐标;
(2)在y轴左侧作直线FG∥y轴,分别交直线AB、直线AC于点F、G,当FG=3DE时,过点G作直线GH⊥y轴于点H,在直线GH上找一点P,使|PF﹣PO|的值最大,求出P点的坐标及|PF﹣PO|的最大值;
(3)将一个45°角的顶点Q放在x轴上,使其角的一边经过A点,另一边交直线AC于点R,当△AQR为等腰直角三角形时,请直接写出点R的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)

-
科目: 来源: 题型:
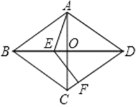
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是线段BO上的一个动点(可以与O、B重合),点F为射线DC上一点,若∠ABC=60,∠AEF=120,AB=5,则EF的取值范围是_____.
相关试题

