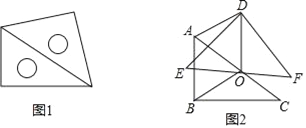
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD.
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)四边形ABOD是菱形,理由见解析.
【解析】试题分析:(1)根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC,由直角三角形斜边上的中线性质得出OB=![]() AC=OA,OD=
AC=OA,OD=![]() EF=
EF=![]() AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;
AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;
(2)由全等三角形的性质得出AB=AD=OB=OD,即可得出四边形ABOD是菱形.
试题解析:(1)证明:根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC.
∵O为AC的中点,∴OB=![]() AC=OA,OD=
AC=OA,OD=![]() EF=
EF=![]() AC=OB,OD⊥EF,∴△AOB是等边三角形,∴∠AOB=60°,AB=OB=OA,由旋转的性质得:∠AOE=30°,∴∠AOD=90°﹣30°=60°.
AC=OB,OD⊥EF,∴△AOB是等边三角形,∴∠AOB=60°,AB=OB=OA,由旋转的性质得:∠AOE=30°,∴∠AOD=90°﹣30°=60°.
在△AOB和△AOD中,∵OA=OA,∠AOB=∠AOD=60°,OB=OD,∴△AOB≌△AOD(SAS);
(2)解:四边形ABOD是菱形.理由如下:
∵△AOB≌△AOD,∴AB=AD,∴AB=AD=OB=OD,∴四边形ABOD是菱形.
-
科目: 来源: 题型:
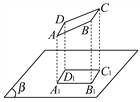
查看答案和解析>>【题目】已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,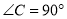 ,
, ,
,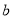 ,
,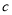 分别是
分别是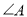 ,
,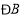 ,
,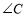 的对边,点
的对边,点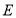 是
是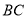 上一个动点(点
上一个动点(点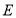 与
与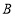 、
、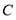 不重合),连
不重合),连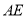 ,若
,若 、
、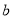 满足
满足 ,且
,且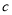 是不等式组
是不等式组 的最大整数解.
的最大整数解.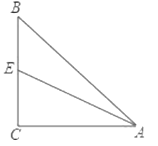
(1)求
 ,
,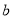 ,
,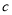 的长;
的长;(2)若
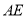 平分
平分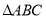 的周长,求
的周长,求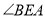 的大小;
的大小;(3)是否存在线段
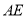 将三角形
将三角形 的周长和面积同时平分?若存在,求出
的周长和面积同时平分?若存在,求出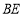 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×5网格图中,其中每个小正方形边长均为1,梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点.
(1)以B为位似中心,在网格图中作四边形A′BC′D′,使四边形A′BC′D′和梯形ABCD位似,且位似比为2:1;
(2)求(1)中四边形A′BC′D′与五边形EFGHK重叠部分的周长.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为_______.

-
科目: 来源: 题型:
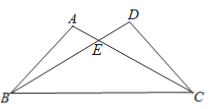
查看答案和解析>>【题目】如图,已知∠A=∠D有下列五个条件①AE=DE ②BE=CE ③AB=DC ④∠ABC=∠DCB⑤AC=BD能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:1.第三组的频数是12.请你回答:
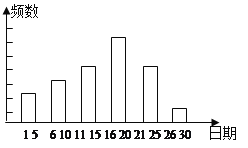
(1)本次活动共有 件作品参赛;
(2)若将各组所占百分比绘制成扇形统计图,那么第四组对应的扇形的圆心角是 度。
(3)本次活动共评出2个一等奖和3个二等奖及三等奖、优秀奖若干名,对一、二等奖作品进行编号并制作成背面完全一致的卡片,背面朝上的放置,随机抽出两张卡片,抽到的作品恰好一个是一等奖,一个是二等奖的概率是多少?
相关试题

