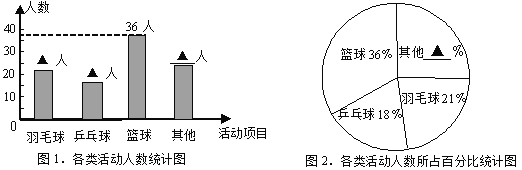
【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、 “羽毛球”、 “乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
(1)学校采用的调查方式是 ;学校共随机选取了 名学生;
(2)补全统计图中的数据:羽毛球 人、乒乓球 人、其他 人、其他 ﹪;
(3)该校共有1100名学生,请估计喜欢“篮球”的学生人数.
参考答案:
【答案】(1)抽样调查 ,100;(2) 21,18,25,25; (3) 396 .
【解析】试题分析:(1)属于抽样调查.根据所占人数÷总人数×100%=百分比,计算即可;
(2)根据百分比公式计算即可;
(3)用样本估计总体的思想解决问题;
试题解析:(1)学校采用的调查方式是抽样调查,
总人数=36÷36%=100(名),
故答案为:抽样调查,100.
(2)条形统计图中羽毛球人数:100×21%=21(人),
乒乓球人数:100×18%=18(人),
扇形统计图中其他占:1﹣36%﹣21%﹣18%=25%,
其他有100×25%=25(人),
故答案为:21,18,25,25%.
(3)1000×18%=180(人),
答:估计喜欢“乒乓球”的学生人数有180人.
-
科目: 来源: 题型:
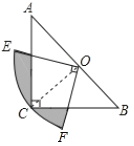
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
-
科目: 来源: 题型:
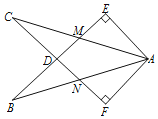
查看答案和解析>>【题目】如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的序号是________.
-
科目: 来源: 题型:
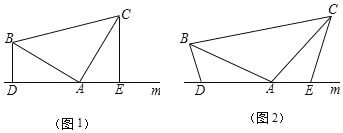
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D, A, E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
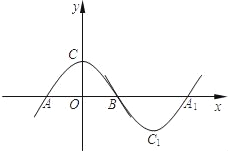
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】丽君花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(2)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少总费用是多少元?
-
科目: 来源: 题型:
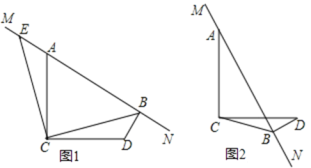
查看答案和解析>>【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC.
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA.
①求证:点E在直线MN上;
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想.
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想.
相关试题

