【题目】丽君花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(2)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少总费用是多少元?
参考答案:
【答案】(1)y=![]() (2)太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元
(2)太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元
【解析】
试题(1)、太阳花的价格=6×数量;绣球花的价格分x≤20和x>20两种情况分别进行计算,得出函数解析式;(2)、首先设太阳花的数量是m盆,则绣球花的数量是(90-m)盆,购买两种花的总费用是w元,根据题意求出m的取值范围,然后得出w与m的函数关系式,然后根据一次函数的增减性得出最小值.
试题解析:(1)、y太阳花=6x;
①y绣球花=10x(x≤20);
②y绣球花=10×20+10×0.8×(x-20)=200+8x-160=8x+40(x>20)
(2)、根据题意, 设太阳花的数量是m盆,则绣球花的数量是(90-m)盆,购买两种花的总费用是w元,
∴m≤![]() (90-m) 则m≤30,
(90-m) 则m≤30,
则w=6m+[8(90-m)+40]=760-2m
∵-2<0 ∴w随着m的增大而减小, ∴当m=30时,
w最小=760-2×30=700(元),
即太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元.
-
科目: 来源: 题型:
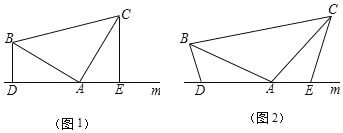
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D, A, E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
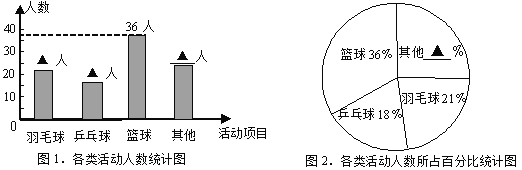
查看答案和解析>>【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、 “羽毛球”、 “乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
(1)学校采用的调查方式是 ;学校共随机选取了 名学生;
(2)补全统计图中的数据:羽毛球 人、乒乓球 人、其他 人、其他 ﹪;
(3)该校共有1100名学生,请估计喜欢“篮球”的学生人数.
-
科目: 来源: 题型:
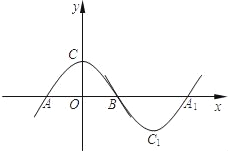
查看答案和解析>>【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
-
科目: 来源: 题型:
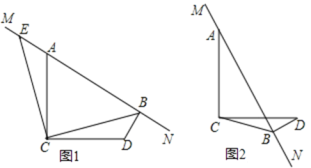
查看答案和解析>>【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC.
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA.
①求证:点E在直线MN上;
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想.
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想.
-
科目: 来源: 题型:
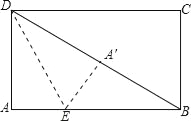
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是( )
A. 1 B.
 C.
C.  D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】有6位同学帮助美术老师装裱美术作品,其中有部分同学装裱过,是熟手,部分同学是生手,每20分钟,熟手可装裱3件,生手可装裱2件,经过2个小时,6位同学共装裱作品84件.
(1)如果设熟手为
 位,那么生手是 位(用
位,那么生手是 位(用 表示)
表示)(2)2小时熟手共装裱 个,生手共装裱 个,(用含
 的代数式表示)
的代数式表示)(3)列方程,求出熟手和生手各几位?
相关试题

