【题目】在平面直角坐标系![]() 中,对于任意三点
中,对于任意三点![]() ,
,![]() ,
,![]() 给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且
给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且![]() ,
,![]() ,
,![]() 三点都在矩形的内部或边界上,那么称该矩形为点
三点都在矩形的内部或边界上,那么称该矩形为点![]() ,
,![]() ,
,![]() 的外延矩形,在点
的外延矩形,在点![]() ,
,![]() ,
,![]() 所有的外延矩形中,面积最小的矩形称为点
所有的外延矩形中,面积最小的矩形称为点![]() ,
,![]() ,
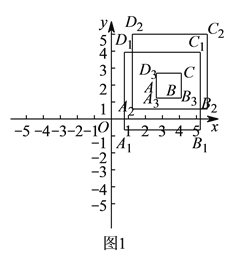
,![]() 的最佳外延矩形.例如,图
的最佳外延矩形.例如,图![]() 中的矩形
中的矩形![]() ,
,![]() ,
,![]() 都是点
都是点![]() ,
,![]() ,
,![]() 的外延矩形,矩形
的外延矩形,矩形![]() 是点
是点![]() ,
,![]() ,
,![]() 的最佳外延矩形.
的最佳外延矩形.
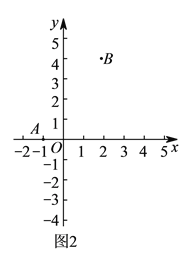
(![]() )如图
)如图![]() ,点
,点![]() ,
,![]() ,
,![]() (
(![]() 为整数).
为整数).
①如果![]() ,则点
,则点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是__________.
的最佳外延矩形的面积是__________.
②如果点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是
的最佳外延矩形的面积是![]() ,且使点
,且使点![]() 在最佳外延矩形的一边上,请写出一个符合题意的
在最佳外延矩形的一边上,请写出一个符合题意的![]() 值__________.
值__________.
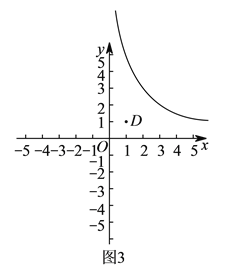
(![]() )如图
)如图![]() ,已知点
,已知点![]() 在函数
在函数![]() 的图象上,且点
的图象上,且点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积
的最佳外延矩形的面积![]() 的取值范围以及该面积最小时
的取值范围以及该面积最小时![]() 的取值范围.
的取值范围.
参考答案:
【答案】(![]() )①
)①![]() .②
.②![]() 或
或![]() .(
.(![]() )
)![]() ,
,![]()
【解析】试题分析:(1)①根据所给的最佳外延矩形的定义求解即可;②由点A(-1,0),B(2,4),可得AB=3,又因最佳外延矩形面积为![]() ,可得最佳外延矩形的另一边长为8,即
,可得最佳外延矩形的另一边长为8,即![]() 或
或![]() ,由此即可求得
,由此即可求得![]() 或
或![]() ;(2)当
;(2)当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() .所以当
.所以当![]() 时,
时,![]() ,当
,当![]() 在其它处位置时,
在其它处位置时,![]() ,由此即可求得结论.
,由此即可求得结论.
试题解析:
(![]() )①当
)①当![]() 时,
时,
最佳外延矩形的面积为![]() .
.
②由最佳外延矩形面积为![]() ,得
,得![]() ,
,
即![]() ,
,
∴![]() ,
,
又∵![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
(![]() )当
)当![]() 时,
时,![]() ,即
,即![]() ,
,
此时![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
此时![]() .
.
∴当![]() 时,
时,![]() ,
,
当![]() 在其它处位置时,
在其它处位置时,![]() ,
,
∴综上![]() ,当
,当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边
 中,
中, ,点
,点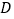 为
为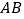 的中点,点
的中点,点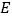 是
是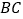 边上一动点,
边上一动点,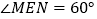 ,且
,且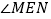 的两边分别与
的两边分别与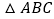 的边
的边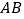 ,
,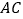 交于点
交于点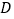 ,
,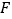 (点
(点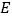 不与点
不与点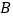 ,
,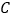 重合).
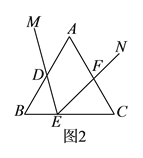
重合).(
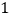 )当
)当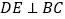 时,请在图
时,请在图 中补全图形.
中补全图形.(
 )在图
)在图 中,设
中,设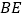 的长为
的长为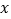 ,
,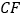 的长为
的长为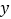 ,求
,求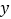 与
与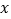 的函数关系式,并写出自变量
的函数关系式,并写出自变量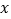 的取值范围.
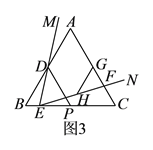
的取值范围.(
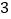 )如图
)如图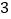 ,点
,点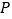 ,
,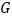 分别为
分别为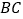 ,
,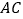 的中点,在
的中点,在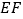 上截取
上截取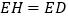 ,连接
,连接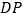 ,
,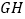 .请证明
.请证明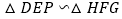 .
.
-
科目: 来源: 题型:
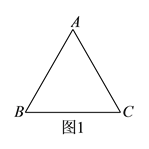
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,过点A作直线DE,且满足BD⊥DE于点D,CE⊥DE于点E,当B,C在直线DE的同侧时,
(1)求证:DE=BD+CE;
(2)如果上面条件不变,当B,C在直线DE的异侧时,如图2,问BD、DE、CE之间的数量关系如何?写出结论并证明
(3)如果上面条件不变,当B,C在直线DE的异侧时,如图3,问BD、DE、CE之间的数量关系如何?写出结论并证明.

-
科目: 来源: 题型:
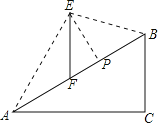
查看答案和解析>>【题目】如图,在坡度
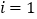 :
: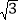 的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为
的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为 ,沿斜坡前进20米到达B,此时测得点E的仰角为
,沿斜坡前进20米到达B,此时测得点E的仰角为 ,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为
,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为 参考数据:
参考数据: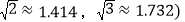
A.
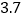 米 B.
米 B. 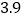 米 C.
米 C. 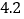 米 D.
米 D. 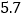 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某学校高中两个班的学生上学时步行、骑车、乘公交、乘私家车人数的扇形统计图,已知乘公交人数是乘私家车人数的2倍.若步行人数是18人,则下列结论正确的是( )

A. 被调查的学生人数为90人
B. 乘私家车的学生人数为9人
C. 乘公交车的学生人数为20人
D. 骑车的学生人数为16人
相关试题

