【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
参考答案:
【答案】(1)∠AOD=135°;(2)∠MON=54°.
【解析】试题分析:(1)根据角平分线的定义求出∠AOC=45°,然后根据邻补角的定义求解即可;
(2)设∠NOB=x°,∠BOC=4x°,根据角平分线的定义表示出∠COM=∠MON=![]() ∠CON,再根据∠BOM列出方程求解x,然后求解即可.
∠CON,再根据∠BOM列出方程求解x,然后求解即可.
(1)∵∠AOM=90°,OC平分∠AOM,∴∠AOC=![]() ∠AOM=
∠AOM=![]() x90°=45°,
x90°=45°,
∵∠AOC+∠AOD=180°,∴∠AOD=180°-∠AOC=180°-45°=135°;
(2)∵∠BOC=4∠NOB,设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,∵OM平分∠CON,
∴∠COM=∠MON=![]() ∠CON=
∠CON=![]() x°,∵∠BOM=
x°,∵∠BOM=![]() x+x=90,∴x=36,
x+x=90,∴x=36,
∴∠MON=![]() x°=54°,即∠MON的度数为54°.
x°=54°,即∠MON的度数为54°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A、0.720精确到百分位 B、5.078×104精确到千分位
C、36万精确到个位 D、2.90×105精确到千位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.
(1)PE的长为 (用含t的代数式表示);
(2)求S与t之间的函数表达式;
(3)求S的最大值及S取得最大值时t的值;
(4)当S为△ABC面积的
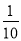 时,t的值有 个.
时,t的值有 个.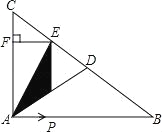
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2016个点的坐标为( )
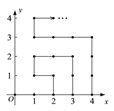
A(45,9) B(45,13) C(45,22) D(45,0)
-
科目: 来源: 题型:
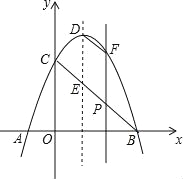
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
(1)求此抛物线所对应的函数表达式.
(2)求PF的长度,用含m的代数式表示.
(3)当四边形PEDF为平行四边形时,求m的值.
-
科目: 来源: 题型:
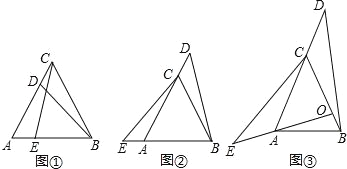
查看答案和解析>>【题目】感知:如图①,在等边三角形ABC中,点D、E分别在边AC、AB上,若AE=CD,易知△ACE≌△CBD.
探究:若图①中的点D、E分别在边AC、BA的延长线上时,如图②,△ACE与△CBD是否仍然全等?如果全等,请证明:如果不全等,请说明理由.
应用:若图②中的等边三角形ABC为等腰三角形,且AC=BC,点O是AC边的垂直平分线与BC的交点,点D、E分别在AC、OA的延长线上,如图③,若AE=CD,∠ACB=α,∠ADB=β,则∠ACE的大小为 (用含α和β的代数式表示).
-
科目: 来源: 题型:
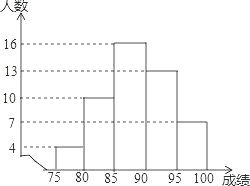
查看答案和解析>>【题目】为了了解某校全体学生参加消防知识竞赛的成绩(均为整数),从中抽取了10%的学生竞赛成绩,整理后绘制如下的频数分布直方图,其中,每组可含量最低值,不含最高值.
根据统计图提供的信息,解答下列问题:
(1)求参加消防知识竞赛的学生总人数.
(2)求抽取的部分学生中竞赛成绩在85~90的频率.
(3)如果竞赛成绩在90分以上(含90分)的同学可以获得奖励,请估计该校全体学生中获得奖励的人数.
相关试题

