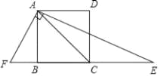
【题目】如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为____.
参考答案:
【答案】2![]()
【解析】
利用正方形的性质和勾股定理可得AC的长,由角平分线的性质和平行线的性质可得∠CAE=∠E,易得CE=CA,由FA⊥AE,可得∠FAC=∠F,易得CF=AC,可得EF的长.
解:∵四边形ABCD为正方形,且边长为1,
∴AC=![]() ,
,
∵AE平分∠CAD,
∴∠CAE=∠DAE,
∵AD∥CE,
∴∠DAE=∠E,
∴∠CAE=∠E,
∴CE=CA=![]() ,
,
∵FA⊥AE,
∴∠FAC+∠CAE=90°,∠F+∠E=90°,
∴∠FAC=∠F,
∴CF=AC=![]() ,
,
∴EF=CF+CE=![]() +
+![]() =2
=2![]() .
.
故答案为:2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

-
科目: 来源: 题型:
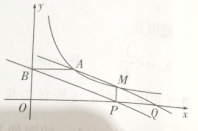
查看答案和解析>>【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y=
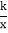 (x>0)的图像上,
(x>0)的图像上,(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.

-
科目: 来源: 题型:
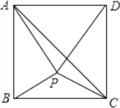
查看答案和解析>>【题目】如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:(1)△APB≌△DPC;(2)∠BAP=2∠PAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 .
.(1)如下图,点
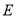 在直线
在直线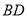 的左侧,请写出
的左侧,请写出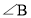 ,
,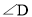 ,
,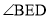 之间的数量关系,并说明理由:
之间的数量关系,并说明理由: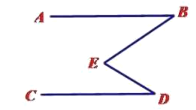
(2)如下图,当点
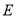 在线段
在线段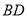 上时,
上时,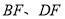 分别平分
分别平分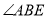 ,
,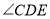 ,此时
,此时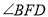 的度数为_________°
的度数为_________°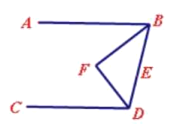
(3)如下图,当点
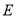 在直线
在直线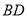 的左侧时,
的左侧时,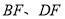 分别平分
分别平分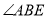 ,
,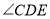 ,请直接写出
,请直接写出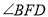 和
和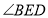 的数量关系 ;
的数量关系 ;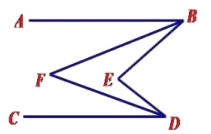
(4)如下图,当点
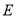 在直线
在直线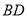 的右侧时,
的右侧时,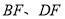 分别平分
分别平分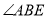 ,
, ,请直接写出
,请直接写出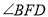 和
和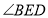 的数量关系 ;
的数量关系 ;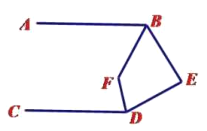
-
科目: 来源: 题型:
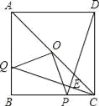
查看答案和解析>>【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
相关试题

