【题目】在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,并事先拟定从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分.
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分.
方案3:所有评委给分的中位数.
方案4:所有评委给分的众数.
为了探究上述方案的合理性,
先对某个同学的演唱成绩进行统计实验,右侧是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分.
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分?
参考答案:
【答案】:解:(1)方案1最后得分:![]() (3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
(3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
方案2最后得分:![]() (7.0+7.8+3×8+3×8.4)=8;
(7.0+7.8+3×8+3×8.4)=8;
方案3最后得分:8;
方案4最后得分:8或8.4.
(2)因为方案1中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,
所以方案1不适合作为最后得分的方案.
因为方案4中的众数有两个,众数失去了实际意义,所以方案4不适合作为最后得分的方案.
【解析】
:本题关键是理解每种方案的计算方法:
(1)方案1:平均数=总分数÷10.
方案2:平均数=去掉一个最高分和一个最低分的总分数÷8.
方案3:10个数据,中位数应是第5个和第6个数据的平均数.
方案4:求出评委给分中,出现次数最多的分数.
(2)考虑不受极值的影响,不能有两个得分等原因进行排除.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.
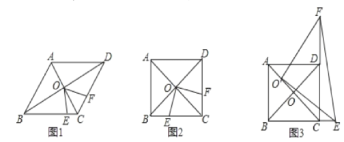
(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系___;
(2)如图1,当∠ABC=90°时,若AC=4
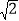 ,BE=
,BE= ,求线段EF的长;
,求线段EF的长;(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,边长为8的正方形OABC的两边在坐标轴上(如图).

(1)求点A,B,C的坐标.
(2)经过A,C两点的直线l上有一点P,点D(0,6)在y轴正半轴上,连PD,PB(如图1),若PB2﹣PD2=24,求四边形PBCD的面积.
(3)若点E(0,1),点N(2,0)(如图2),经过(2)问中的点P有一条平行于y轴的直线m,在直线m上是否存在一点M,使得△MNE为直角三角形?若存在,求M点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌ Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
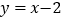 与
与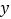 轴交于点C,与
轴交于点C,与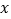 轴交于点B,与反比例函数
轴交于点B,与反比例函数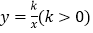 的图象在第一象限交于点A,连接OA,若
的图象在第一象限交于点A,连接OA,若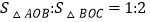 ,则k的值为_____.
,则k的值为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
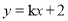 与x轴交于点
与x轴交于点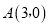 ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线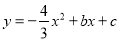 经过点
经过点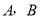 .
.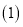 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;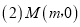 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点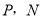 .
. 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.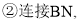 当
当 时,求m的值.
时,求m的值. 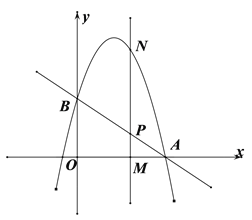
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(写出计算过程)
(1)(-35) + 18 + (-5) + (+22)
(2)

(3)

(4)

(5)

(6)9+5×(-3)-(-2)2÷4
(7)(-22)×(-3)2+(-32)÷4;
(8)﹣32+1÷4×
 ﹣|﹣1
﹣|﹣1 |×(﹣0.5)2
|×(﹣0.5)2
相关试题

