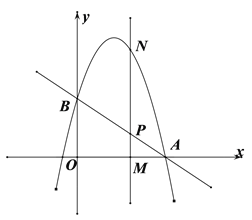
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 当
当![]() 时,求m的值.
时,求m的值.
参考答案:
【答案】⑴![]() ,
, ![]() ⑵
⑵![]() ⑶有两解,N点在AB的上方或下方, m=
⑶有两解,N点在AB的上方或下方, m=![]() 与m=
与m=![]()
【解析】整体分析:
(1)把A(3,0)代入y=kx+2中求k值,把x=0代入y=kx+2,求出B点的坐标,由A,B的坐标求二次函数的解析式;(2)①用含m的式子表示出NP的长,由平行四边形的性质得OB=PN列方程求解;②连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H, 设GH=BH=t,由![]() ,用t表示AH,AG,由AB=
,用t表示AH,AG,由AB=![]() ,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
解:⑴![]() ,
,
二次函数的表达式为![]()
⑵如图,设M(m,0),
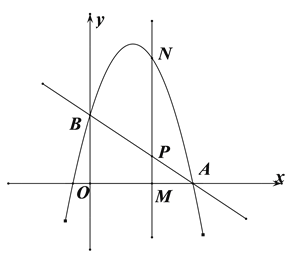
则p(m, ![]() ),N(m,
),N(m, ![]()
![]() =
=![]()
=![]()
由于四边形OBNP为平行四边形得PN=OB=2,
解方程![]() .
.
即![]()
⑶有两解,N点在AB的上方或下方,m=![]() 与m=
与m=![]() .
.
如图连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H.
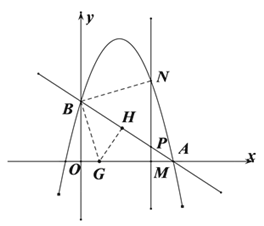
由![]() 得
得![]() ,
,
从而设GH=BH=t,则由![]() ,得AH=
,得AH= ![]() ,
,
由AB=t+ ![]() =
=![]() ,解得t=
,解得t=![]() ,
,
从而OG=OA-AG=3-![]() =
=![]() .即G(
.即G(![]() )
)
由B(0,2),G(![]() )得
)得![]() .
.
将![]() 分别与
分别与![]() 联立,
联立,
解方程组得m=![]() ,m=
,m=![]() .
.
故m=![]() 与m=
与m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌ Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,并事先拟定从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分.
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分.
方案3:所有评委给分的中位数.
方案4:所有评委给分的众数.
为了探究上述方案的合理性,
先对某个同学的演唱成绩进行统计实验,右侧是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分.
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分?

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
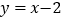 与
与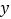 轴交于点C,与
轴交于点C,与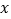 轴交于点B,与反比例函数
轴交于点B,与反比例函数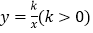 的图象在第一象限交于点A,连接OA,若
的图象在第一象限交于点A,连接OA,若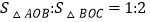 ,则k的值为_____.
,则k的值为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(写出计算过程)
(1)(-35) + 18 + (-5) + (+22)
(2)

(3)

(4)

(5)

(6)9+5×(-3)-(-2)2÷4
(7)(-22)×(-3)2+(-32)÷4;
(8)﹣32+1÷4×
 ﹣|﹣1
﹣|﹣1 |×(﹣0.5)2
|×(﹣0.5)2 -
科目: 来源: 题型:
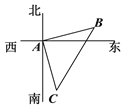
查看答案和解析>>【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1
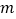 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区很多学校开展了大课间活动.某校初三(1)班抽查了10名同学每分钟仰卧起坐的次数,数据如下(单位:次):51,69,64,52,64,72,48,52,76,52.
(1)这组数据的众数为 ______;求这组数据的中位数;
(2)在对初三(2)班10名同学每分钟仰卧起坐次数的抽查中,已知这组数据的平均数正好与初三(1)班上述数据的平均数相同,且除众数(唯一)之外的6个数之和为348.求这组数据的众数.
相关试题

