【题目】菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.
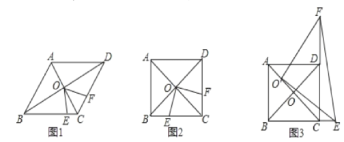
(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系___;
(2)如图1,当∠ABC=90°时,若AC=4![]() ,BE=
,BE=![]() ,求线段EF的长;
,求线段EF的长;
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
参考答案:
【答案】(1)CE+CF=![]() AB;(2)
AB;(2)![]() ;(3)CFCE =
;(3)CFCE =![]() O`C.
O`C.
【解析】
(1)如图1中,连接EF,在CO上截取CN=CF,只要证明△OFN≌△EFC,即可推出CE+CF=OC,再证明OC=![]() AB即可.
AB即可.
(2)先证明△OBE≌△OCF得到BE=CF,在Rt△CEF中,根据CE![]() +CF
+CF![]() =EF
=EF![]() 即可解决问题.
即可解决问题.
(3)结论:CF-CE=![]() O`C,过点O`作O`H⊥AC交CF于H,只要证明△FO`H≌△EO
O`C,过点O`作O`H⊥AC交CF于H,只要证明△FO`H≌△EO![]() C,推出FH=CE,再根据等腰直角三角形性质即可解决问题.
C,推出FH=CE,再根据等腰直角三角形性质即可解决问题.
(1)结论CE+CF=![]() AB.
AB.
理由:如图1中,连接EF,在CO上截取CN=CF.

∵∠EOF+∠ECF=180°,
∴O、E. C. F四点共圆,
∵∠ABC=60°,四边形ABCD是菱形,
∴∠BCD=180°∠ABC=120°,
∴∠ACB=∠ACD=60°,
∴∠OEF=∠OCF,∠OFE=∠OCE,
∴∠OEF=∠OFE=60°,
∴△OEF是等边三角形,
∴OF=FE,
∵CN=CF,∠FCN=60°,
∴△CFN是等边三角形,
∴FN=FC,∠OFE=∠CFN,
∴∠OFN=∠EFC,
在△OFN和△EFC中,
 ,
,
∴△OFN≌△EFC,
∴ON=EC,
∴CE+CF=CN+ON=OC,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠CBO=30°,AC⊥BD,
在RT△BOC中,∵∠BOC=90°,∠OBC=30°,
∴OC=![]() BC=
BC=![]() AB,
AB,
∴CE+CF=![]() AB.
AB.
(2)连接EF

∵在菱形ABCD中
∴菱形ABCD是正方形,
∴∠BOC=90°,OB=OC,AB=AC,∠OBE=∠OCF=45°,∠BCD=90°
∵∠EOF+∠BCD=180°,
∴∠EOF=90°,
∴∠BOE=∠COF
∴△OBE≌△OCF,
∴BE=CF,
∵BE=![]() ,
,
∴CF=![]() ,
,
在Rt△ABC中,AB![]() +BC
+BC![]() =AC
=AC![]() ,AC=4
,AC=4![]()
∴BC=4,
∴CE=![]() ,
,
在Rt△CEF中,CE![]() +CF
+CF![]() =EF
=EF![]() ,
,
∴EF=![]()
答:线段EF的长为![]() ,
,
(3)结论:CFCE=![]() O`C.
O`C.
理由:过点O`作O`H⊥AC交CF于H,

∵∠O`CH=∠O`HC=45°,
∴O`H=O`C,
∵∠FO`E=∠HO`C,
∴∠FO`H=∠CO`E,
∵∠EO`F=∠ECF=90°,
∴O`.C. F. E四点共圆,
∴∠O`EF=∠OCF=45°,
∴∠O`FE=∠O`EF=45°,
∴O`E=O`F,
在△FO`H和△EO`C中,
 ,
,
∴△FO`H≌△EO![]() C,
C,
∴FH=CE,
∴CFCE=CFFH=CH=![]() O`C.
O`C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(直接写结果)
(1)- 5+ 2 =
(2)-5-2=
(3)5-(-2)=
(4)(-5)×(-2)=
(5)(-2)÷(-6)=
(6)
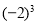 =
=(7)
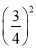 =
= (8)
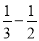 =
= (9)
 =
= (10)
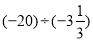 =
= -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元)
5
10
15
20
50
捐款人数(人)
7
18
10
12
3
(1)求这50个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A、B两种计算器共100个,要求A种计算器数量不低于B种的
 ,且不高于B种的
,且不高于B种的 .已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.
.已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.(1)求计划购买这两种计算器所需费用y(元)与x的函数关系式;
(2)问该公司按计划购买者两种计算器有多少种方案?
(3)由于市场行情波动,实际购买时,A种计算器单价下调了3m(m>0)元/个,同时B种计算器单价上调了2m元/个,此时购买这两种计算器所需最少费用为12150元,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,边长为8的正方形OABC的两边在坐标轴上(如图).

(1)求点A,B,C的坐标.
(2)经过A,C两点的直线l上有一点P,点D(0,6)在y轴正半轴上,连PD,PB(如图1),若PB2﹣PD2=24,求四边形PBCD的面积.
(3)若点E(0,1),点N(2,0)(如图2),经过(2)问中的点P有一条平行于y轴的直线m,在直线m上是否存在一点M,使得△MNE为直角三角形?若存在,求M点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌ Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,并事先拟定从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分.
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分.
方案3:所有评委给分的中位数.
方案4:所有评委给分的众数.
为了探究上述方案的合理性,
先对某个同学的演唱成绩进行统计实验,右侧是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分.
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分?

相关试题

