Question

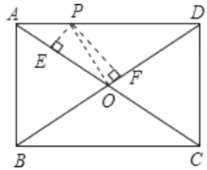
【题目】如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是__．

Answer 1

【答案】4.8

【解析】

首先连接OP，由矩形的两条边AB、BC的长分别为6和8，可求得OA＝OD＝5，△AOD的面积，然后由S△AOD＝S△AOP＋S△DOP＝OAPE＋ODPF求得答案．

解：连接OP，
∵矩形的两条边AB、BC的长分别为6和8，
∴S矩形ABCD＝ABBC＝48，OA＝OC，OB＝OD，AC＝BD＝，
∴OA＝OD＝5，
∴S△ACD＝S矩形ABCD＝24，
∴S△AOD＝S△ACD＝12，
∵S△AOD＝S△AOP＋S△DOP＝OAPE＋ODPF＝×5×PE＋×5×PF＝（PE＋PF）＝12，
解得：PE＋PF＝4.8．
故答案为：4.8．