【题目】已知二次函数y=x2-2mx+m2-1.

(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
参考答案:
【答案】(1)二次函数的解析式为:y=x2-2x或y=x2+2x;(2)C(0,3)、D(2,-1);(3)P(![]() ,0).
,0).
【解析】
试题分析:(1)根据二次函数的图象经过坐标原点O(0,0),直接代入求出m的值即可;
(2)根据m=2,代入求出二次函数解析式,进而利用配方法求出顶点坐标以及图象与y轴交点即可;
(3)根据当P、C、D共线时PC+PD最短,利用平行线分线段成比例定理得出PO的长即可得出答案.
试题解析:(1)∵二次函数的图象经过坐标原点O(0,0),
∴代入二次函数y=x2-2mx+m2-1,得出:m2-1=0,
解得:m=±1,
∴二次函数的解析式为:y=x2-2x或y=x2+2x;
(2)∵m=2,
∴二次函数y=x2-2mx+m2-1得:y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点为:D(2,-1),
当x=0时,y=3,
∴C点坐标为:(0,3),
∴C(0,3)、D(2,-1);
(3)当P、C、D共线时PC+PD最短,
过点D作DE⊥y轴于点E,
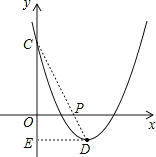
∵PO∥DE,
∴![]() ,
,
∴![]() ,
,
解得:PO=![]() ,
,
∴PC+PD最短时,P点的坐标为:P(![]() ,0).
,0).
-
科目: 来源: 题型:
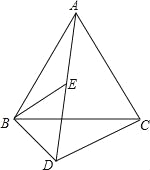
查看答案和解析>>【题目】如图,已知△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明DA﹣DB=DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队计划参与一项工程建设,甲队单独施工
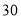 天完成该项工程的
天完成该项工程的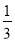 ,这时乙队加入,两队还需同时施工
,这时乙队加入,两队还需同时施工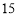 天,才能完成该项工程.
天,才能完成该项工程.(1)若乙队单独施工,需要多少天才能完成该项工程;
(2)若甲队参与该项工程施工的时间不超过
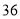 天,则乙队至少施工多少天才能完成该项工程?
天,则乙队至少施工多少天才能完成该项工程? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AB交x轴于点A(4 ,0),交y轴于点B(0 ,4),
(1)如图,若C的坐标为(-1, ,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(2)在(1)的条件下,如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连结MD,过点D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,式子
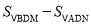 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.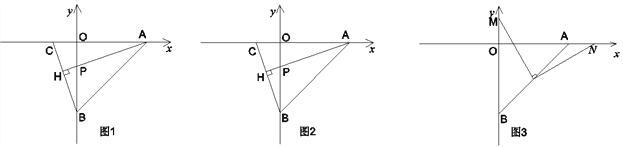
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形
 的底边
的底边 长为
长为 ,面积是
,面积是 , 腰
, 腰 的垂直平分线
的垂直平分线 分别交
分别交 边于
边于 点.若点
点.若点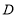 为
为 边的中点,点
边的中点,点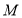 为线段EF上一动点,则
为线段EF上一动点,则 周长的最小值为( )
周长的最小值为( )
A.
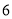 B.
B. C.
C. D.
D.
相关试题

