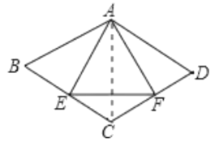
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A.2![]() cmB.3
cmB.3![]() cmC.4
cmC.4![]() cmD.3cm
cmD.3cm
参考答案:
【答案】B
【解析】
首先根据菱形的性质证明△ABE≌△ADF,然后连接AC可推出△ABC以及△ACD为等边三角形.根据等腰三角形三线合一的定理又可推出△AEF是等边三角形.根据勾股定理可求出AE的长继而求出周长.
解:连接AC,
∵四边形ABCD是菱形,
∴AB=AD=BC=CD,∠B=∠D,
∵E、F分别是BC、CD的中点,
∴BE=DF,
在△ABE和△ADF中,
AB=AD,∠B=∠D,BE=DF,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF.
∵∠B=∠D=60°,
∴△ABC与△ACD是等边三角形,
∴AE⊥BC,AF⊥CD(等腰三角形底边上的中线与底边上的高线重合),
∴∠BAE=∠DAF=30°,
∴∠EAF=60°,
∴△AEF是等边三角形.
∴AE=![]() cm,
cm,
∴周长是3![]() cm.
cm.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0.
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根;
(2)当Rt△ABC的斜边长a为
 ,且两条直角边的长b和c恰好是这个方程的两个根时,求△ABC的周长.
,且两条直角边的长b和c恰好是这个方程的两个根时,求△ABC的周长. -
科目: 来源: 题型:
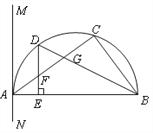
查看答案和解析>>【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出图中的立体图形的名称.

①_______;②_______;③_______;④_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)

(1)求收工时距A地多远?
(2)在第______次纪录时距A地最远。
(3)若每千米耗油0.3升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-2mx+m2-1.

(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
相关试题

