【题目】如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD=

参考答案:
【答案】25.
【解析】
试题分析:过A点作AF⊥CD交CD的延长线于F点,由AE⊥BC,AF⊥CF,∠C=90°可得四边形AECF为矩形,则∠2+∠3=90°,而∠BAD=90°,根据等角的余角相等得∠1=∠2,加上∠AEB=∠AFD=90°和AB=AD,根据全等三角形的判定可得△ABE≌△ADF,由全等三角形的性质有AE=AF=5,S△ABE=S△ADF,则S四边形ABCD=S正方形AECF,然后根据正方形的面积公式计算即可.
试题解析:过A点作AF⊥CD交CD的延长线于F点,如图,
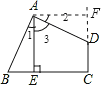
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠2,
在△ABE和△ADF中
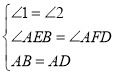
∴△ABE≌△ADF,
∴AE=AF=5,S△ABE=S△ADF,
∴四边形AECF是边长为5的正方形,
∴S四边形ABCD=S正方形AECF=52=25.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF= 度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数yl=x(x≥0),
 (x>0)的图象如图所示,则结论: ①两函数图象的交点A的坐标为(3,3);
(x>0)的图象如图所示,则结论: ①两函数图象的交点A的坐标为(3,3);
②当x>3时,y2>y1;
③当x=1时,BC=8;
④当x逐渐增大时,yl随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简
(1) +|﹣2|﹣4sin45°﹣(
+|﹣2|﹣4sin45°﹣(  )﹣1
)﹣1
(2)解方程 ﹣
﹣  =
=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
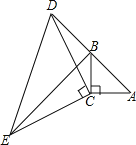
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=2cm,则BE=_______cm.
(3)BE与AD有何位置关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
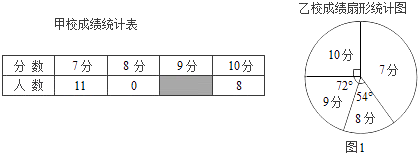
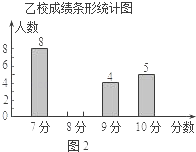
(1)在图1中,“7分”所在扇形的圆心角等于°.
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
相关试题

