【题目】某商场有一种游戏,规则是:在一只装有8个红球和若干个白球(每个球除颜色外都相同)的不透明的箱子中,随机摸出1个球,摸到红球就可获得一瓶饮料.工作人员统计了参加游戏的人数和获得饮料的人数(见下表).
(1)计算并完成表格;
参加游戏的人数 | 200 | 300 | 400 | 500 |
获得饮料的人数 | 39 | 63 | 82 | 99 |
获得饮料的频率 |
(2)估计获得饮料的概率;
(3)请你估计袋中白球的数量.
参考答案:
【答案】(1)0.195,0.21,0.205,0.198;(2)0.2;(3)估计袋中有32个白球.
【解析】
(1)用获得饮料的人数除以参加游戏的人数即可得;
(2)根据(1)中的频率进行估计即可;
(3)利用估计的概率和概率公式进行求解即可.
(1)39÷200=0.195,63÷300=0.21,82÷400=0.202,99÷500=0.198,
填表如下:
参加游戏的人数 | 200 | 300 | 400 | 500 |
获得饮料的人数 | 39 | 63 | 82 | 99 |
获得饮料的频率 | 0.195 | 0.21 | 0.205 | 0.198 |
(2)观察表格可知随着参加人数的增加,获得饮料的频率逐渐稳定在0.2附近,
所以估计获得饮料的概率为0.2;
(3)设袋中有白球x个,
根据题意,得![]() ,
,
解这个方程,得x=32,
经检验,x=32是所列方程的解,
答:估计袋中有32个白球.
-
科目: 来源: 题型:
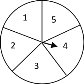
查看答案和解析>>【题目】如图,转盘中5个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,把下列事件:①指针落在标有3的区域内;②指针落在标有奇数的区域;③指针落在标有6的区域内;④指针落在标有偶数或奇数的区域,的序号按发生的可能性从小到大的顺序排列为_____.
-
科目: 来源: 题型:
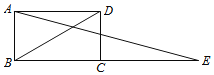
查看答案和解析>>【题目】如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ABD=m°,则∠E=_____度(用含m的代数式表示).
-
科目: 来源: 题型:
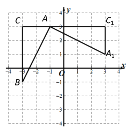
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(-1,3)、B(-3,-1)、C(-3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,0)和B(0,b)满足
 ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:① ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若 ,则
,则 ;其中正确的有( )
;其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
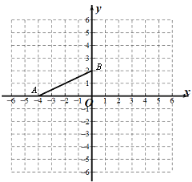
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(-4,0)、B(0,2),点P(a,a).
(1)当a=2时,将△AOB绕点P(a,a)逆时针旋转90°得△DEF,点A的对应点为D,点O的对应点为E,点B的对应点为点F,在平面直角坐标系中画出△DEF,并写出点D的坐标 ;
(2)作线段AB关于P点的中心对称图形(点A、B的对应点分别是G、H),若四边形ABGH是正方形,则a= .
相关试题

