【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
参考答案:
【答案】D
【解析】∵AB=AC,D为BC中点,
∴CD=BD,∠BDO=∠CDO=90°,
在△ABD和△ACD中, ,
,
∴△ABD≌△ACD;
∵EF垂直平分AC,
∴OA=OC,AE=CE,
在△AOE和△COE中,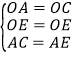 ,
,
∴△AOE≌△COE;
在△BOD和△COD中,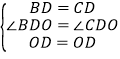 ,
,
∴△BOD≌△COD;
在△AOC和△AOB中, ,
,
∴△AOC≌△AOB;
故选:D.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等),还要掌握等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m﹣5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=
 x的图象如图所示,它与二次函数y=ax2﹣4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.
x的图象如图所示,它与二次函数y=ax2﹣4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.
(1)求点C的坐标
(2)设二次函数图象的顶点为D.
①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式;
②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.

(1)若∠AOB=60°,OM=4,OQ=1,求证:CN⊥OB
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ﹣
﹣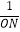 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1 , △NOC的面积为S2 , 求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式:

(2)计算: ÷(a+2﹣
÷(a+2﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加社团的情况,从2010年起,某市教育部门每年都从全市所有学生中随机抽取2000名学生进行调查,图①、图②是部分调查数据的统计图(参加社团的学生每人只能报一项)根据统计图提供的信息解决下列问题:

(1)求图②中“科技类”所在扇形的圆心角α的度数
(2)该市2012年抽取的学生中,参加体育类与理财类社团的学生共有多少人?
(3)该市2014年共有50000名学生,请你估计该市2014年参加社团的学生人数.
相关试题

