【题目】(1)解不等式:
(2)计算:![]() ÷(a+2﹣
÷(a+2﹣![]() )
)
参考答案:
【答案】解:(1)由x﹣1>2x,可得x<﹣1,
由![]() ,可得x<﹣8,
,可得x<﹣8,
∴不等式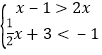 的解集是:
的解集是:
x<﹣8.
(2)![]() ÷(a+2﹣
÷(a+2﹣![]() )
)
=![]() ÷
÷![]()
=﹣![]()
【解析】(1)根据一元一次不等式组的解法,首先求出每个不等式的解集,再求出这些解集的公共部分即可.
(2)根据分式的混合运算顺序,首先计算小括号里面的,然后计算除法,求出算式![]() ÷(a+2﹣
÷(a+2﹣![]() )的值是多少即可.
)的值是多少即可.
【考点精析】通过灵活运用分式的混合运算和一元一次不等式组的解法,掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.

(1)若∠AOB=60°,OM=4,OQ=1,求证:CN⊥OB
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ﹣
﹣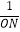 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1 , △NOC的面积为S2 , 求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )

A.1对
B.2对
C.3对
D.4对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加社团的情况,从2010年起,某市教育部门每年都从全市所有学生中随机抽取2000名学生进行调查,图①、图②是部分调查数据的统计图(参加社团的学生每人只能报一项)根据统计图提供的信息解决下列问题:

(1)求图②中“科技类”所在扇形的圆心角α的度数
(2)该市2012年抽取的学生中,参加体育类与理财类社团的学生共有多少人?
(3)该市2014年共有50000名学生,请你估计该市2014年参加社团的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m、n的值
(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上

(1)求斜坡AB的水平宽度BC。
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高。( ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)
相关试题

