Question

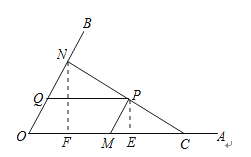
【题目】如图，C为∠AOB的边OA上一点，OC=6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．

（1）若∠AOB=60°，OM=4，OQ=1，求证：CN⊥OB
（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
①问：﹣的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
②设菱形OMPQ的面积为S1 ， △NOC的面积为S2 ， 求的取值范围．

Answer 1

【答案】
（1）

解：（1）过P作PE⊥OA于E，

∵PQ∥OA，PM∥OB，

∴四边形OMPQ为平行四边形，

∴PM=OQ=1，∠PME=∠AOB=60°，

∴PE=PMsin60°=，ME=，

∴CE=OC﹣OM﹣ME=，

∴tan∠PCE==，

∴∠PCE=30°，

∴∠CPM=90°，

又∵PM∥OB，

∴∠CNO=∠CPM=90°，

则CN⊥OB

（2）

解：

①﹣的值不发生变化，理由如下：

设OM=x，ON=y，

∵四边形OMPQ为菱形，

∴OQ=QP=OM=x，NQ=y﹣x，

∵PQ∥OA，

∴∠NQP=∠O，

又∵∠QNP=∠ONC，

∴△NQP∽△NOC，

∴=，即=，

∴6y﹣6x=xy．两边都除以6xy，得﹣=，即﹣=．

②过P作PE⊥OA于E，过N作NF⊥OA于F，

则S1=OMPE，S2=OCNF，

∴=．

∵PM∥OB，

∴∠PMC=∠O，

又∵∠PCM=∠NCO，

∴△CPM∽△CNO，

∴==，

∴==﹣（x﹣3）2+，

∵0＜x＜6，

则根据二次函数的图象可知，0＜≤．

【解析】（1）过P作PE⊥OA于E，利用两组对边平行的四边形为平行四边形得到OMPQ为平行四边形，利用平行四边形的对边相等，对角相等得到PM=OQ=1，∠PME=∠AOB=60°，进而求出PE与ME的长，得到CE的长，求出tan∠PCE的值，利用特殊角的三角函数值求出∠PCE的度数，得到PM于NC垂直，而PM与ON平行，即可得到CN与OB垂直；
（2）﹣的值不发生变化，理由如下：设OM=x，ON=y，根据OMPQ为菱形，得到PM=PQ=OQ=x，QN=y﹣x，根据平行得到三角形NQP与三角形NOC相似，由相似得比例即可确定出所求式子的值；
②过P作PE⊥OA于E，过N作NF⊥OA于F，表示出菱形OMPQ的面积为S1 ， △NOC的面积为S2 ， 得到，由PM与OB平行，得到三角形CPM与三角形CNO相似，由相似得比例求出所求式子的范围即可．
【考点精析】关于本题考查的相似三角形的应用，需要了解测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解才能得出正确答案．