【题目】为积极响应政府提出的“绿色发展低碳出行”号召,某自行车厂决定生产一批共享单车投入市场.该厂原计划一周生产1400辆共享单车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

⑴根据记录可知前三天共生产 辆;
⑵产量最多的一天比产量最少的一天多生产 辆;
⑶该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
参考答案:
【答案】(1)599;(2)26;(3)84675元
【解析】
(1)根据有理数的加法,可得答案;
(2)根据最大数减最小数,可得答案;
(3)根据实际生产的量乘以单价,可得工资,根据超出的部分或不足的部分乘以每辆的奖金,可得奖金,根据工资加奖金,可得答案.
解:(1)+5+(-2)+(-4)=5+(-6)=-1,200×3+(-1)=600-1=599(辆),
∴前三天共生产599辆;
(2)观察可知,星期六生产最多,星期五生产最少,
+16-(-10)=16+10=26(辆),
∴产量最多的一天比产量最少的一天多生产26辆;
(3)+5+(-2)+(-4)+(+13)+(-10)+(+16)+(-9)
=5-2-4+13-10+16-9
=5+13+16-2-4-10-9
=34-25
=9,
∴工人这一周的工资总额是:(1400+9)×60+9×15=84540+135=84675(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:|a|=3,b2=4,ab<0,求a﹣b的值.
(2)已知关于x的方程
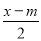 =
=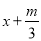 与方程
与方程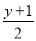 =3y﹣2的解互为倒数,求m的值.
=3y﹣2的解互为倒数,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是边长为4的正方形,E为AB的中点,将△ADE绕点D沿逆时针方向旋转后得到△DCF,连接EF,则EF的长为( )

A. 2
 B. 2
B. 2 C. 2
C. 2 D. 2
D. 2
-
科目: 来源: 题型:
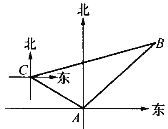
查看答案和解析>>【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时15
 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=
 ,且OC=4,求BD的长.
,且OC=4,求BD的长.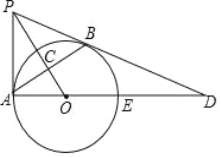
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD平分∠ACB交AB于点D,E为AC上一点,且DE∥BC

(1)求证:DE=CE;
(2)若∠A=90°,S△BCD=26,BC=13,求AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,在正方形ABCD中,点E在对角线AC上(不与点A、C重合),连结ED,EB,过点E作EF⊥ED,交边BC于点F.易知∠EFC+∠EDC=180°,进而证出EB=EF.
探究:如图②,点E在射线CA上(不与点A、C重合),连结ED、EB,过点E作EF⊥ED,交CB的延长线于点F.求证:EB=EF
应用:如图②,若DE=2,CD=1,则四边形EFCD的面积为
相关试题

