【题目】(1)已知:|a|=3,b2=4,ab<0,求a﹣b的值.
(2)已知关于x的方程![]() =
=![]() 与方程
与方程![]() =3y﹣2的解互为倒数,求m的值.
=3y﹣2的解互为倒数,求m的值.
参考答案:
【答案】(1)5或﹣5;(2)m=﹣![]() .
.
【解析】
(1)根据“|a|=3,b2=4”结合绝对值的定义和有理数的乘方的定义,再结合ab<0,求出a和b的值,列式计算即可,
(2)根据解一元一次方程基本步骤,求出方程![]() =3y﹣2的解,根据“x的方程
=3y﹣2的解,根据“x的方程![]() =
=![]() 与方程
与方程![]() =3y﹣2的解互为倒数”,求出x的值,代入方程
=3y﹣2的解互为倒数”,求出x的值,代入方程![]() =
=![]() 得到关于m的一元一次方程,解之即可.
得到关于m的一元一次方程,解之即可.
(1)∵|a|=3,
∴a=3或﹣3,
∵b2=4,
∴b=2或﹣2,
又∵ab<0,
∴![]() 或
或![]() ,
,
a﹣b=3﹣(﹣2)=5或a﹣b=﹣3﹣2=﹣5,
即a﹣b的值为5或﹣5,
(2)解方程![]() =3y﹣2得:y=1,
=3y﹣2得:y=1,
根据题意得:x=1,
把x=1代入方程![]() =
=![]() 得:
得:
![]() ,
,
解得:m=﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下结论:①单项式﹣
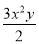 的系数为﹣
的系数为﹣ ,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+
,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+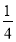 )﹣2(x﹣
)﹣2(x﹣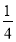 )的结果是﹣x+
)的结果是﹣x+ ;④若单项式
;④若单项式 ax2yn+1与﹣
ax2yn+1与﹣ axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是边长为4的正方形,E为AB的中点,将△ADE绕点D沿逆时针方向旋转后得到△DCF,连接EF,则EF的长为( )

A. 2
 B. 2
B. 2 C. 2
C. 2 D. 2
D. 2
-
科目: 来源: 题型:
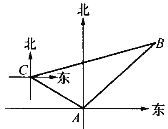
查看答案和解析>>【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时15
 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展低碳出行”号召,某自行车厂决定生产一批共享单车投入市场.该厂原计划一周生产1400辆共享单车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

⑴根据记录可知前三天共生产 辆;
⑵产量最多的一天比产量最少的一天多生产 辆;
⑶该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
相关试题

